トップ   編集 凍結解除 差分 バックアップ 添付 複製 名前変更 リロード   新規 一覧 単語検索   ヘルプ   最終更新のRSS

MATLAB Note/音声の分析

Last-modified: 2018-01-29 (月) 14:24:41
Top / MATLAB Note / 音声の分析

音声を取り込む・再生する †

  • WAVREAD Microsoft WAVE (".wav") サウンドファイルの読み込み -> WAVREADは2018年1月現在無効 
    filename = 'a.wav';                    %読み込むファイル名を指定
[data,Fs,Bits] = wavread(filename);    %dataに音声データ、Fsにはサンプリング周波数を代入
sound(data,Fs);            %サンプリング周波数 Fs で再生
wavplay(data,Fs);          %サンプリング周波数 Fs でWindows のオーディオ出力を使って再生
wavplay(data,Fs,'async');  %音声の再生に平行して処理を続行する
disp('再生中...');
  • AUDIOREAD Microsoft WAVE (".wav") サウンドファイルの読み込み 
    filename = 'a.wav';                    %読み込むファイル名を指定
[data,Fs] = audioread(filename);    %dataに音声データ、Fsにはサンプリング周波数を代入
sound(data,Fs);            %サンプリング周波数 Fs で再生
player = audioplayer(data,Fs);
play(player);          %サンプリング周波数 Fs でWindows のオーディオ出力を使って再生
  • デフォルトで、以下のような音声データが用意されています。 
    load laughter;      %笑い声
sound(y, Fs);

load handel;        %handelのハレルヤ
sound(y, Fs);

load mtlb;          %MATLABと発音した英語音声
sound(mtlb,Fs);
↑

波形をプロットする †

  • 取り込んだ波形をプロットするには 
    load mtlb;          %MATLABと発音した音声をロード（変数mtlbがデータ、Fsがサンプリング周波数）
plot(mtlb);
  • 44Hzの正弦波を作って、波形をプロットするには 
    Fs = 8192;			%サンプリング周波数 8192[Hz]
f = 44;   			%周波数（音の高さ）44[Hz]
A = 1.0;   			%振幅（音の大きさ）1.0
length = 0.5; 			%音の再生時間 0.5[秒]
timeline = 0 : 1/Fs : length; 		%時間軸の作成 1/Fs 間隔で0～length[秒]まで
data = A * sin(2 * pi * f * timeline);  %正弦波信号を生成
subplot(2,1,1); plot(data, '.')	%ドットでプロット
subplot(2,1,2); plot(data)		%通常のプロット
title('時間信号'), xlabel('time');	%グラフのラベル
↑

スペクトログラム †

  • スペクトログラムは、パワースペクトル解析の結果を時間軸上にプロットしたものです（時間：横軸、周波数：縦軸、パワー：色の濃さ）。 → 参考
  • 「MATLAB」と発音したサンプル英語音声を取り込んでプロットする 
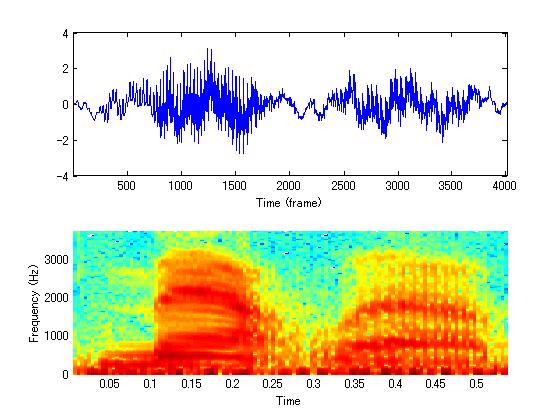
     load mtlb;          %MATLABと発音した英語音声
 disp(strcat('サンプリング周波数は',  int2str(Fs), '[Hz] サウンドデータは mtlb'));
 sound(mtlb, Fs)     %再生
 wavwrite(mtlb, Fs, 32, 'mtlb.wav'); %量子化ビット数32でファイル書き出し
 subplot(2,1,1);
 plot(mtlb); xlabel('Time (sample)'); xlim([1 length(mtlb)]); ylabel('振幅');
 subplot(2,1,2);
 spectrogram(mtlb, hamming(64), 32, 256, Fs, 'yaxis'); %スペクトログラム
 % 64 サンプル（Wavesurferと同じ）の対称なHamming窓で分割して処理
 % 32 サンプルのオーバーラップ
 % 256 サンプルのFFT長
    • 実行結果（音声波形とスペクトログラム）
      mtlb_mfcc_1.jpg
      • 元の音声のサンプリング周波数と量子化ビット数によって、スペクトログラムの細かさ（y軸・x軸の解像度）が変わってきますので、Hamming窓の長さ、オーバーラップのサンプル数、FFT長の値を調整してください。
  • マイクから2.0秒間音を取り込んで、取り込んだ音声のスペクトログラムを表示するには、以下のようにします。 
    Fs = 44100;  time = 2.0;
data  = wavrecord(time*Fs, Fs, 1);                     %1chでtime秒間録音する
spectrogram(data, hamming(64), 32, 256, Fs, 'yaxis');  %スペクトログラムをプロット

% 64 点（Wavesurferと同じ）のHamming窓で解析する、細かいほど正確になります。
% mtlb の各セグメントが 32 点のオーバーラップをする
% 離散フーリエ変換を計算するために使われる周波数点数は 256
% yaxis ： y軸上に周波数をプロットする
  • スペクトログラムからある瞬間（1、50、100 フレーム）におけるパワースペクトルを知るには、以下のようにします。 
    load mtlb;    %MATLABにはじめからセットされている英語音声をロード
subplot(3,2,[1 2 3 4]);
spectrogram(mtlb, hamming(64), 32, 256, Fs, 'yaxis');
[s,f,t,p] = spectrogram(mtlb, hamming(64), 32, 256, Fs, 'yaxis');
% f : スペクトログラムにおける周波数ベクトル
% t : 時間ベクトル
% p : 各セグメントのパワースペクトル密度 
subplot(3,2,[5 6]);
plot([1:length(p)], p(:,1), [1:length(p)], p(:,50), [1:length(p)], p(:,100) );
legend('segment = 1', 'segment = 50', 'segment = 100');
xlabel('周波数'); ylabel('パワー');
↑

音声波形のフレーム分割および前処理 †

  • 音声解析の前準備として、音声の高域強調・フレーム分割・窓関数による丸めといった処理を行う方法を説明します。
↑

高域強調（プリエンファシス） †

  • 音声信号は低周波数成分が大きく、周波数が大きくなるにつれて次第に振幅スペクトルが小さくなっていくという特徴がある。この周波数の偏りの修正処理をプリエンファシスという。*1
  • 声帯の基本振動、空気中の伝搬の影響を除き、口腔内の形状による周波数特性を強調する処理である（法政大伊藤先生 ケプストラムを用いた母音の分析）
  • プリエンファシスを行うことで、第二・第三フォルマントのような高次周波数成分の抽出性能が向上する。雑音下においては、雑音除去の処理を行った後でプリエンファシスを行うことが一般的。*2
  • 具体的には、ハイパスフィルタを使い、高周波数成分の振幅を強調する処理を行う。
    • 式は以下のとおり。
      a math image
      • x(n)はサンプル数nを変数とするデジタルサウンドデータ（音声波形）
      • pはプリエンファシス係数。音声認識では0.97を使うことが多い。
      • １サンプル前の値に対して、大きく値が変化した場合（高周波数成分）、その値は保存される。値の変化が小さかった場合（低周波数成分）、その値は減じられる。
    • MATLAB では以下のようにする。 
       load mtlb;
 data = mtlb;
 pre_emphasis = 0.97;    %プリエンファシス係数

 newData = [];
 for countData = 2 : 1 : length(data)
     %プリエンファシス
     thisData = data(countData) - ( pre_emphasis * data(countData - 1) );
     newData = [newData ; thisData ];
 end

 subplot(2,2,1); plot(data); xlim([0,4500]); title('元のサウンドデータ');
 subplot(2,2,2); spectrogram(data, hamming(64), 32, 256, Fs, 'yaxis'); 
 subplot(2,2,3); plot(newData); xlim([0,4500]); title('プリエンファシス後');
 subplot(2,2,4); spectrogram(newData, hamming(64), 32, 256, Fs, 'yaxis'); 
 wavwrite(newData, Fs, 'newmtlb.wav');
  • 以下の関数でも同じ処理ができる。 
     newData = filter([1 -0.97],1,data);
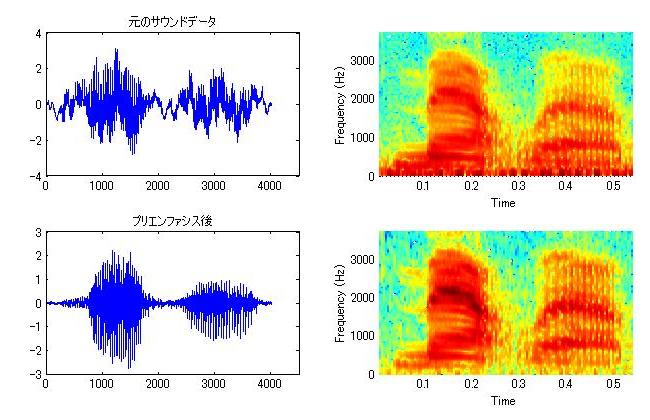
  • プリエンファシスの結果は以下のようになる。
mtlb_mfcc_5.jpg
  • 基本周波数成分（スペクトログラム下部のボイスバーの部分）が除去されていること、高次フォルマントの成分が強調されていることなどが分かる。
↑

フレーム切り出し †

  • 連続音声の分析を行う場合は、音声信号を短い時間単位で切り出す必要がある。この時間単位をフレームと呼ぶ。
    • 1フレーム内に2周期程度の音声信号が含まれていれば、うまく音声情報を取り出すことができる。
    • 通常フレーム同士は重複するようにとる。重複部分の長さをフレームのシフト長とよぶ。
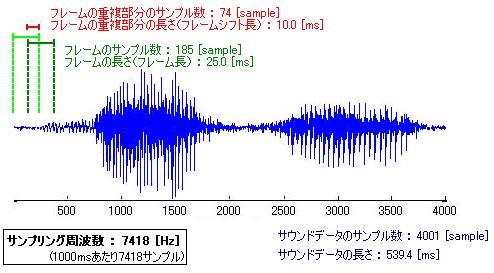
  • 例えば、お題の音声を、音声認識で一般的に用いられる フレーム長25ms、フレームシフト長10msで切り出す場合、以下のようになる。
mtlb_mfcc_2.jpg
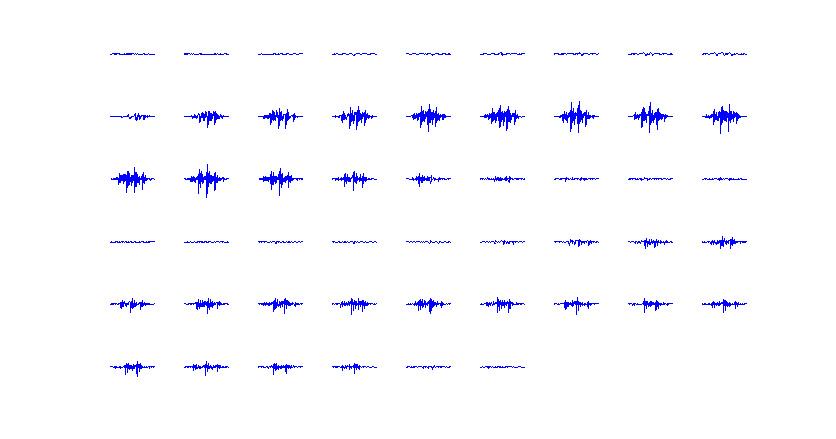
  • 以下のコードで、フレームの切り出しを行う（2010.05.11.フレーム総数計算の間違いを修正しました。）。 
     frameSize = 0.025;               % フレーム長：0.025秒（25ms）
 frameShift = 0.010;              % フレームシフト長：0.010秒（10ms）

 load mtlb;
 data = mtlb;

 data = filter([1 -0.97],1,data);     %プリエンファシス

 frameSizeSample = fix( Fs * frameSize );        % フレーム長：サンプル換算
 frameShiftSample = fix( Fs * frameShift );      % フレームシフト長：サンプル換算
 disp( strcat('サウンドデータのサンプル数 ',int2str(length(data)),'[sample], ',...
     'フレーム長 ',int2str(frameSizeSample),'[sample], ',...
     'フレームシフト長 ',int2str(frameShiftSample),'[sample]') );

 %フレームの総数を求める
 maxFrame = ...
  fix( ( length(data) - (frameSizeSample - frameShiftSample) ) / frameShiftSample ) - 1;

 %フレームの個数だけ処理を繰り返す
 startThisFrame = 1;                                  % フレームの開始サンプル番号
 endThisFrame = startThisFrame + frameSizeSample - 1; % フレームの終了サンプル番号
 for countFrame = 1 : 1 : maxFrame
     disp(strcat('フレーム番号 ',int2str(countFrame),' / ',int2str(maxFrame)));
     disp(strcat('このフレームの開始サンプル番号 ',num2str(startThisFrame)));
     disp(strcat('このフレームの終了サンプル番号 ',num2str(endThisFrame)));
     thisData = data(startThisFrame : endThisFrame);

     % ここでこのフレームに対する計算を行う
     subplot(6, 9, countFrame); plot(thisData); ylim([-3,3]);
    axis off; %目盛りを消す

     startThisFrame = startThisFrame + frameShiftSample;
    endThisFrame = startThisFrame + frameSizeSample - 1;
 end
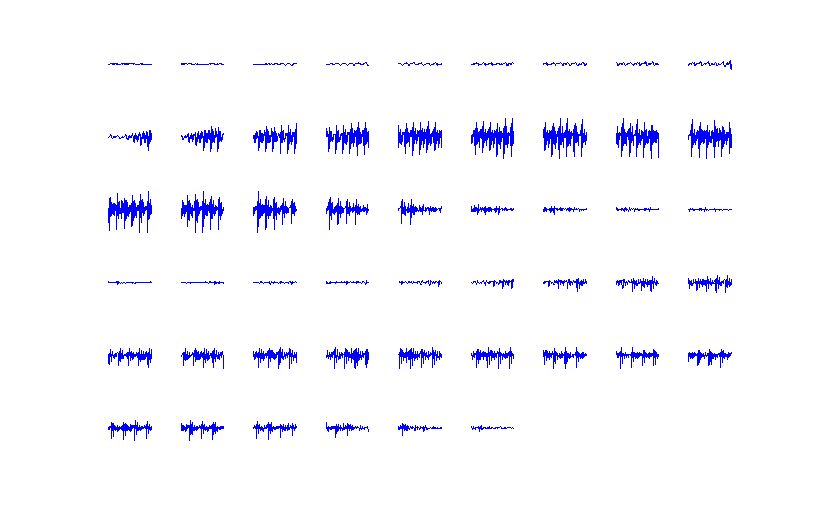
  • 結果は以下のようになる。51個のフレームに切り出された。
mtlb_mfcc_3.png
↑

窓関数による丸め †

  • 上で取り出したフレームは、単純に音声波形を切り出しただけのものであるため、波形のはじまりと終わりが不連続に途切れていて、後述するフーリエ変換を使う際に不都合が生じる。
    • そのため、上で切り出した音声に窓関数をかけあわせて、切り出し境界部分を滑らかにする。
  • ここでは、ハミング窓を使う。
    • ハミング窓は以下の式で表わされる*3。
      a math image
      • MATLABでは以下の関数を使って作ることができる。 
         frameSizeSample = 185;              % フレーム長：サンプル換算
 window = hamming(frameSizeSample);  % ハミング窓を生成
 plot(window);
  • 前述のスクリプトにハミング窓をかけてみる。
    • mtlb_mfcc_1.m を実行する。
    • 結果は以下のようになる。
mtlb_mfcc_4.png
  • 各フレームの角がまるまっている。
↑

パワースペクトル解析 †

↑

パワースペクトルによるホワイトノイズの検出 †

  • 音声のパワースペクトルは低周波数成分のパワーが大きく、白色雑音は全周波数帯のパワーが等しいことを利用して、雑音部の自動抽出ができます。
    fileanalyzeNoize.m
↑

線形予測法（LPC）とフォルマント解析 †

  • FFTによって出力されたスペクトル解析の結果をみると、小さな周期性（基本周波数）のほかに、大きなスペクトルの山が確認できたと思います。これをスペクトル包絡とよびます。
    • スペクトル包絡の山は、音声の声道に由来する周波数成分です。詳しくは メル周波数ケプストラム（MFCC） を参照してください。
    • 音声では、スペクトル包絡の山の頂点がフォルマント周波数に対応します。
  • スペクトル包絡をより明確に求めたい場合、線形予測法（LPC）を使います。
    • filea.wav を使って以下のコードを実行 
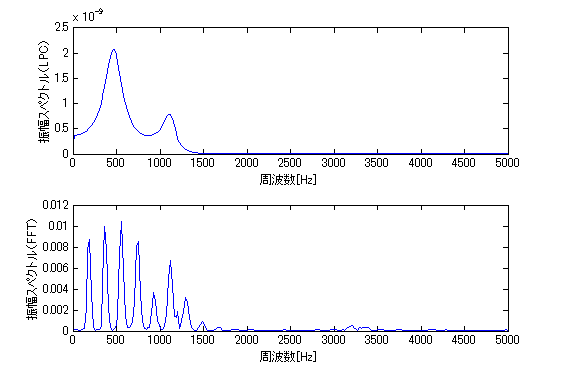
      [wav, Fs] = wavread('a.wav');
%中央部分を切り出し
center = fix(length(wav) / 2);   %中心のサンプル番号
cuttime = 0.04;                  %切り出す長さ[s]
wavdata = wav(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));

%ハニング窓をかける
han_window = 0.5 - 0.5 * cos(2 * pi * [0 : 1/length(wavdata) : 1]);
wavdata = han_window(1:length(wavdata))' .* wavdata;

lpcsize = 32;     %LPC次数
fftsize = 2048;   %フーリエ変換の次数, 周波数ポイントの数

[P,f] = pyulear(wavdata, lpcsize, fftsize, Fs);  %LPC分析
AP = abs(P) / fftsize;                           %振幅スペクトル

%プロット
fscale = linspace(0, Fs, fftsize);    %0～Fsまでをfftsize個に分割
%プロット（表示するのはサンプリング周波数の半分まで）
subplot(2,1,1); plot(fscale(1:fftsize/2), AP(1:fftsize/2)); 
xlabel('周波数[Hz]'); ylabel('振幅スペクトル（LPC）'); xlim([0,5000]);

dft = fft(wavdata, fftsize);                     %比較用のフーリエ変換
Adft = abs(dft) / fftsize;                       %振幅スペクトル
subplot(2,1,2); plot(fscale(1:fftsize/2), Adft(1:fftsize/2)); 
xlabel('周波数[Hz]'); ylabel('振幅スペクトル（FFT）'); xlim([0,5000]);
    • 結果
      lpc_01.png
      • スペクトル包絡が取り出せました。
  • スペクトル包絡のピークピッキングによって、フォルマント周波数を調べます。
    • 上記のコードに続いて、以下を実行します。 
      peakNum = [];  %ピークのフレーム番号
for peakcount = 2 : 1 : (length(AP)-1)
  if ((AP(peakcount) >= AP(peakcount-1)) & (AP(peakcount) >= AP(peakcount+1))) 
     peakNum(peakcount) = 1;        % ピークのところだけ1を代入
  end
end
peakposition = find(peakNum == 1);  % ピークの位置を決定
fmag = AP(peakposition);            % 振幅を求める
frequences = f(peakposition);       % フォルマント周波数を求める

if (length(frequences) >= 1)
  F1 = frequences(1);               % 第一フォルマント
end
if (length(frequences) >= 2)
  F2 = frequences(2);               % 第二フォルマント
end
if (length(frequences) >= 3)
  F3 = frequences(3);               % 第三フォルマント
end

disp(strcat('F1 : ', num2str(F1), ' F2 : ', num2str(F2), ' F3 : ', num2str(F3)))
    • 結果 
      F1 :473.7305 F2 :1098.1934 F3 :3337.6465
      • 小さな値から第一フォルマント、第二フォルマント、第三フォルマント … の周波数が取り出せています。 → 横軸のスケールとfの値が 1/2 になっていないか？要確認!!
      • なお、ここで得られる値は確実にフォルマントを取り出せているとは限りません。無声区間を分析してしまったエラーは、frequences の平均値が閾値以下になったら除外するなどして除去できます。f1をf2で置換してしまったなどのエラーは、得られた値をプロットするなどして除去する必要があります。
↑

基本周波数解析*4 †

  • filea.wav を使って以下のコードを実行 
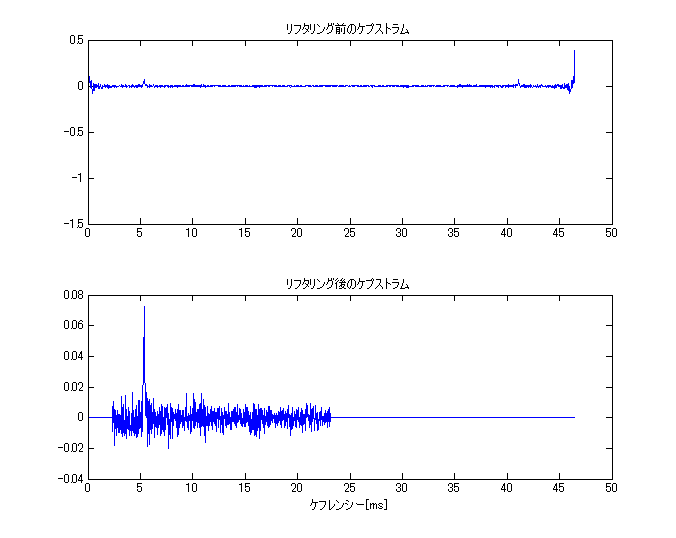
    [wav, Fs] = wavread('a.wav');
t = 0 : 1/Fs : length(wav)/Fs;
%中央部分を切り出し
center = fix(length(wav) / 2);   %中心のサンプル番号
cuttime = 0.04;                  %切り出す長さ[s]
wavdata = wav(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));
time = t(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));

%ハニング窓をかける
han_window = 0.5 - 0.5 * cos(2 * pi * [0 : 1/length(wavdata) : 1]);
wavdata = han_window(1:length(wavdata))' .* wavdata;

fftsize = 2048;                        % フーリエ変換の次数, 周波数ポイントの数
dft = fft(wavdata, fftsize);           % 離散フーリエ変換
Adft = abs(dft);                       % 振幅スペクトル
Adft_log = log10(abs(dft));            % 対数振幅スペクトル
cps = real(ifft( Adft_log ));          % ケプストラム

quefrency = linspace(0, cuttime*2, cuttime*Fs*2);	%ケフレンシー軸、0[s]～切り出した音声の長さの2倍[s]までをサンプル数で分割（2倍にしたのはfftsizeより多くの点をとるため）

subplot(2,1,1); plot(quefrency(1:length(cps))*1000, cps); title('リフタリング前のケプストラム');

%基本周波数ピーク抽出
cps(1:length(cps)/20) = 0;             % ケプストラムの低次成分を除去する（リフタリング）
cps(fftsize/2:fftsize) = 0;            % ケプストラムの後半を除去する

subplot(2,1,2); plot(quefrency(1:length(cps))*1000, cps); title('リフタリング後のケプストラム');
xlabel('ケフレンシー[ms]');
    • 結果
      cps_001.png
    • 上図の低次成分を除去した結果が下図です。基本周波数のピークが確認できます。
  • ピークのケフレンシーの値を求め、周波数[Hz]に変換します。 
    peakQuefrency = quefrency( find(cps == max(cps)) );
f0 = 1 / peakQuefrency;
disp(f0);
    • 結果 
      185.2416
    • Praatで a.wav のピッチを解析した結果 filea_pitch_praat.txt と、ほぼ一致しています。
    • より正確に求めるには、閾値などを決めてエラー検出をする必要があります。
  • 自己相関による方法
    • 長所 ： ノイズに強い（ロバスト）　短所 ： ケプストラムと比べるとやや不正確
↑

メルケプストラム解析 †

  • MATLABでメルケプストラム解析を実行するには、Malcolm Slaney 氏が開発したフリーのMATLABパッケージ Auditory Toolbox を使います。
  • 結果は以下のようになります。
    mfcc_1.png
  • 【補足1】mfcc.m でのフレーム長・フレームシフト長について
    • フレーム長は定数値を与えており、mfcc.m の40行目「windowSize = 256;」で、「フレーム長を256サンプルとする」と定義しています。「256サンプル」が何秒になるかは、サンプリングレート（Fs）によって変わります。上の例では、 Fsは7418（1秒間に7418サンプル）なので、フレーム長は256/7418=約0.035秒です。
    • フレームシフト長は mfcc.m の引数である samplingRate, frameRate によって決定されます。
      • frameRate は「1秒間をいくつのフレームに分割するか」を意味しています。
      • mfcc.m の111行目「windowStep = samplingRate/frameRate;」で、 windowStep の値は「1秒間をいくつのフレームに分割するか」 「1フレームあたりのサンプル数」を意味しています。
      • 上の例では、frameRateは100を指定していますから、「1秒間を74.18100個のフレームに分割する」ことになります。フレームシフト長は 1/74.18=約0.013秒 1/100=0.01秒 です。
    • mfcc.m の112行目「cols = fix((length(input)-windowSize)/windowStep);」は解析するデータの総フレーム数です。上の例では、 size(mfcc_data) = [12 50] になり、12次元のMFCCが50フレーム出力されます。colsの値も50になります。
  • 【補足2】フレーム長 0.025秒、フレームシフト長 0.010秒 で解析するには
    • WindowSize の値を Fs * 0.025 に書き換えます。
    • フレームシフト長は1/100秒（1秒を100のフレームに分割）なので、frameRate = 100 を引数で与えます。
↑

フィルタバンク解析 †

  • フィルタバンク解析とは
    • フィルタバンク：バンドパスフィルタの集合体。入力信号を特定の数の帯域に分割する。
    • 重要でない帯域のサンプリング周波数を減らし、再び結合することで、情報圧縮に利用できる。*6
    • 各帯域のスペクトルの積分を求めることで、スペクトルの次数を帯域の数と同じに圧縮する手法、ともいえる。*7
  • 以下のフィルタバンク解析において、バンドパスフィルタの設計手法は MATLAB 音声信号処理（北海道大 豊村先生）を参考にしています。
↑

2分割フィルタバンク*8 †

  • 以下のようにします。 
     load handel;
 n = 150;                                % 150次のローパスデジタルフィルタ
 bandpassWidth = [1 2000 ; 2001 4000];   % 1～2000Hzと、2001～4000Hzの２分割
 %順番に処理する
 subplotcount = 1;
 for count = 1 : 1 : length(bandpassWidth)
     % インパルス応答を求める
     Wn = [ bandpassWidth(count,1)/(Fs/2) bandpassWidth(count,2)/(Fs/2) ];
     b = fir1(n,Wn,'bandpass');
     % ゲイン特性を求める
     [h,w] = freqz(b,1,512);
     subplot(length(bandpassWidth),3,subplotcount);
     plot((w/pi)*(Fs/2),abs(h)); xlabel('Hz'); legend('ゲイン特性');
     subplotcount = subplotcount + 1;
     % フィルタをかける
     y2 = filter(b,1,y);                 % フィルタをかけた後の波形
     subplot(length(bandpassWidth),3,[subplotcount subplotcount+1]);
     specgram(y2,512,Fs,kaiser(500,5),475);
     subplotcount = subplotcount + 2;
 end
    • 結果は以下のようになります。
      filter10.png
↑

オクターブフィルタバンク（オクターブバンド）*9*10 †

  • まず、オクターブバンドの各フィルタのインパルス応答とゲイン特性を求めてみます。
    • あらかじめ、指定したベクトルの中で、指定した値に一番近い値の番号を出力する関数 filegetNearNum.m を同じディレクトリに入れておきます。
    • 以下を実行します。 
       Fs = 8192;      % サンプリング周波数（load handel の Fs の値を指定）
 n = 150;        % 150次のローパスデジタルフィルタ
 octWidth = 1/1; % フィルタバンクの幅（オクターブ）

 %周波数スケール軸と、オクターブスケール軸を定義する
 freqScale = (0:10:Fs/2);            % 1Hzから10Hzおきに、ナイキスト周波数まで
 octaveScale = log2(freqScale + 1);  % 周波数が二倍になったら１オクターブ上がる

 %バンドパスフィルタの幅を決める
 bandpassFreq = [];
 for count = min(octaveScale) : octWidth : max(octaveScale)
     startOct = count;                 % このフィルタの開始オクターブ値
     endOct = count + octWidth;        % このフィルタの終了オクターブ値
     % ベクトルoctaveScaleの中で、startOctに最も近い値の番号を得る
     [startNum startData] = getNearNum(octaveScale, startOct);
     % ベクトルoctaveScaleの中で、endOctに最も近い値の番号を得る
     [endNum endData] = getNearNum(octaveScale, endOct);
     % 周波数スケールに変換
     %  開始周波数が終了周波数より小さいとき（周波数が小さいときに起こる）を除去
     if (freqScale(startNum) < freqScale(endNum))
         bandpassFreq = [bandpassFreq ; freqScale(startNum) freqScale(endNum)];
     end
 end

 %各フィルタバンクのインパルス応答とゲイン特性を求める
 bBank = [];
 hBank = [];
 wBank = [];
 for count = 1 : 1 : length(bandpassFreq)
     % インパルス応答を求める
     Wn = [ bandpassFreq(count,1)/(Fs/2) bandpassFreq(count,2)/(Fs/2) ];
     b = fir1(n,Wn,'bandpass');
     bBank = [bBank ; b];
     % ゲイン特性を求める
     [h,w] = freqz(b,1,512);
     hBank = [hBank h];
     wBank = [wBank w];
 end

 % ゲイン特性をプロットする
 filtersize = length(bandpassFreq);                         % フィルタの数
 set(gcf,'DefaultAxesColorOrder', [linspace(0,1,filtersize)'...
  linspace(0.5,0,filtersize)' linspace(1,0,filtersize)']);  % 色を指定
 subplot(2,1,1); plot((wBank/pi)*(Fs/2),abs(hBank));
 xlim([min(freqScale) max(freqScale)]); 
 xlabel('周波数[Hz]');
 title( strcat(num2str(octWidth), 'オクターブフィルタバンク') );
 subplot(2,1,2); plot( log2((wBank/pi)*(Fs/2)), abs(hBank) );
 xlim([min(octaveScale) max(octaveScale)]);
 xlabel('オクターブ');
    • 実行結果は以下のようになります（1/1オクターブフィルタバンク）。
filter12.png
  • 周波数軸上で対数間隔、オクターブスケール上で等間隔にフィルタが作られていることが分かります。
  • 低い周波数では、ゲイン特性が予想とは異なる形になってしまっています（原因を要検討！）。
  • 1/3オクターブフィルタバンクを作りたいときは、変数octWidthの値を1/3に変えます。実行結果は以下のとおり。
filter13.png
  • フィルタバンクに音声データを入力します。
    • 以下を実行します。 
       load handel;

 % 順番に処理する
 yAll = [];
 for count = 1 : 1 : filtersize
     % フィルタをかける
     y2 = filter(bBank(count,:),1,y);
     yAll = [yAll y2];
     % プロット
     subplot((filtersize/2),2,count);
     specgram(y2,512,Fs,kaiser(500,5),475);
 end
    • 結果は以下のようになります。
filter14.png
  • フィルタの1番目（ bBank(1,:) ）は、全てNaNのため出力もありません（原因を要検討！）。
  • なお、7番目～10番目のフィルタのゲイン応答と、出力波形のスペクトログラムは以下のようになっています。
    filter11.png
  • 分割した出力波形を足しあわせて、もとの波形を再現することもできます。 
     yAllSize = size(yAll);
 wav = sum(yAll(:, 2:yAllSize(2)),2);    % 1番目のフィルタの出力はNaNなので除く
 wavplay(wav,Fs);                        % 再生
 specgram(wav,512,Fs,kaiser(500,5),475); % スペクトログラム
↑

メルフィルタバンク*12 †

  • メルスケールとは？
  • メルバンドの各フィルタのインパルス応答とゲイン特性を求めます。
    • はじめに、メルスケールの変換関数 mellog.m と、指定したベクトルの中で指定した値に一番近い値の番号を出力する関数 getNearNum.m を同じディレクトリに入れておきます。
    • 以下を実行します。*13 
       Fs = 8192;           % サンプリング周波数（load handel の Fs の値を指定）
 n = 150;             % 150次のローパスデジタルフィルタ
 melFilterNum = 20;   % フィルタバンクの分割数

 %周波数スケール軸と、メルスケール軸を定義する
 freqScale = (1:10:Fs/2);            % 1Hzから10Hzおきに、ナイキスト周波数まで
 melScale = mellog(freqScale);

 %フィルタバンクの幅を求める
 % メルスケール上で等間隔、ただし半分は隣と重複しているので(分割数/2+0.5)で割る
 % 最後に足す0.5は右端の三角窓の右半分の長さ
 melWidth = max(melScale) / ( melFilterNum / 2 + 0.5 );

 %バンドパスフィルタの幅を決める
 bandpassFreq = [];
 countFilterNum = 0;
 for count = min(melScale) : melWidth/2 : max(melScale)
     countFilterNum = countFilterNum + 1;
     if countFilterNum <= melFilterNum
         startMel = count;                 % このフィルタの開始メル値
         endMel = count + melWidth;        % このフィルタの終了メル値
         % ベクトルmelScaleの中で、startMelに最も近い値の番号を得る
         [startNum startData] = getNearNum(melScale, startMel);
         % ベクトルmelScaleの中で、endMelに最も近い値の番号を得る
         [endNum endData] = getNearNum(melScale, endMel);
         % 周波数スケールに変換
         bandpassFreq = [bandpassFreq ; freqScale(startNum) freqScale(endNum)];
     end
 end

 %各フィルタバンクのインパルス応答とゲイン特性を求める
 mBank = [];
 bBank = [];
 hBank = [];
 wBank = [];
 for count = 1 : 1 : length(bandpassFreq)
     % 三角窓のゲイン特性を作る
     startFreq = bandpassFreq(count,1);
     endFreq = bandpassFreq(count,2);
     % 10Hzおきに、長さ(endFreq - startFreq)Hzの三角窓を作る
     triWin = triang((endFreq - startFreq)/10)';
     % ゲインの値を初期化
     m = zeros(1,length(freqScale));
     % startFreqHzからendFreqHzの区間のゲインを triWin に置き換え
     m(ceil(startFreq/10):ceil(endFreq/10-1)) = triWin;
     mBank = [mBank ; m];

     % 周波数軸を0～1の範囲に修正
     f = freqScale - min(freqScale);    % 最小を0に
     f = f / max(f);                    % 最大を1に
     % インパルス応答を求める
     b = fir2(n,f,m);
     bBank = [bBank ; b];
     % ゲイン特性を求める
     [h,w] = freqz(b,1,512);
     hBank = [hBank h];
     wBank = [wBank w];
 end

 % ゲイン特性をプロットする
 filtersize = length(bandpassFreq);                         % フィルタの数
 set(gcf,'DefaultAxesColorOrder', [linspace(0,1,filtersize)'...
  linspace(0.5,0,filtersize)' linspace(1,0,filtersize)']);  % 色を指定
 subplot(3,1,1); plot(freqScale, mBank);
 title( strcat(num2str(melWidth), 'メルフィルタバンク') );
 xlim([min(freqScale) max(freqScale)]); 
 xlabel('周波数[Hz](理想応答)');
 subplot(3,1,2); plot((wBank/pi)*(Fs/2),abs(hBank));
 xlim([min(freqScale) max(freqScale)]); 
 xlabel('周波数[Hz](fir2による設計)');
 subplot(3,1,3); plot( mellog((wBank/pi)*(Fs/2)), abs(hBank) );
 xlim([min(melScale) max(melScale)]);
 xlabel('メル[mel]');
    • 結果は以下のようになります。
filter15.png
  • メル周波数スケール上で等間隔な、20個のバンドパスフィルタができました（分割数を変えたいときは、変数 melFilterNum の値を変えます）。*14
  • 周波数スケール上では、低周波数成分ほど幅の狭い（＝周波数解像度の高い）フィルタになっています。
  • 隣の三角窓と半分重複しているのは、音声認識の特徴量の慣例です。
  • フィルタバンクに音声データを入力します。
    • 以下を実行します。 
       load handel;

 % 順番に処理する
 yAll = [];
 for count = 1 : 1 : filtersize
     % フィルタをかける
     y2 = filter(bBank(count,:),1,y);
     yAll = [yAll y2];
     % プロット
     subplot((filtersize/4),4,count);
     specgram(y2,512,Fs,kaiser(500,5),475);
 end
    • 結果は以下のようになります。
filter16.png
  • 分割した出力波形を足しあわせて、もとの波形を再現することもできます。
↑

メルフィルタバンク解析（音声波形を分割するやり方） †

  • 上で分割した出力波形からMFCCを求めてみます。
  • まず、それぞれの帯域の出力波形のスペクトル解析を行い、振幅スペクトルの和を求めて*15各帯域につき１つの振幅スペクトルの値を求めます。*16
    • スペクトル解析のスクリプト（サウンドデータにハニング窓をかけて、プリエンファシスして、振幅スペクトルを求める）calcSpectrum.m を同じディレクトリに入れておきます。
    • 上に続けて、以下を実行します（このスクリプトでは、handel の中心 0.04秒のみ取り出して解析しています）。 
       % 切り出した各帯域の音声波形の中央部分を切り出して、振幅スペクトルの和を求める
 cuttime = 0.04;                     %切り出す長さ[s]
 timeScale = 0 : 1/Fs : length(y)/Fs;
 pre_emphasis = 0.97;                %プリエンファシス係数
 fftsize = 2048;                     %フーリエ変換の次数, 周波数ポイントの数
 fscale = linspace(0, Fs, fftsize);  %周波数スケール（0～Fsをfftsizeに分割）
 AdftSum = [];
 for count = 1 : 1 : filtersize
     wav = yAll(:,count);

     % 中央部分を切り出し
     center = fix(length(thisWav) / 2);   %中心のサンプル番号
     wavdata = wav(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));
     time = timeScale(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));
     figure(1); subplot((filtersize/4),4,count);
     plot(time*1000, wavdata); xlabel('時間[ms]');

     % 振幅スペクトルを求め、和をとる
     Adft = calcSpectrum( wavdata, fftsize, pre_emphasis );
     figure(2); subplot((filtersize/4),4,count);
     plot(fscale(1:fftsize/2), Adft(1:fftsize/2)); xlim([0,5000]);
     AdftSum = [AdftSum sum(Adft)];
 end
    • 結果は以下のようになります。
      • 帯域ごとに切り出した音声波形
filter17.png
  • 各帯域の振幅スペクトル
    filter18.png
  • 続いて、20次元に圧縮された振幅スペクトルをプロットします。 
     %フィルタバンクによって melFilterNum 次元に圧縮された対数振幅スペクトルを求める
 bandpassMedianFreq = median(bandpassFreq,2);    % バンドパスフィルタの中心周波数
 AdftSum_log = log10(AdftSum);
 %  比較用、もとの音声波形の振幅スペクトルと対数振幅スペクトル
 center = fix(length(y) / 2);
 wavdata = y(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));
 time = timeScale(center-fix(cuttime/2*Fs) : center+fix(cuttime/2*Fs));
 Adft = calcSpectrum( wavdata, fftsize, pre_emphasis ); Adft_log = log10(Adft);
 figure(3);
 subplot(2,2,1); plot(fscale(1:fftsize/2), Adft(1:fftsize/2));
 xlim([0,5000]); title(strcat('もとの音声波形の振幅スペクトル'));
 subplot(2,2,2); plot(fscale(1:fftsize/2), Adft_log(1:fftsize/2));
 xlim([0,5000]); title(strcat('もとの音声波形の対数振幅スペクトル'));
 subplot(2,2,3); plot(bandpassMedianFreq, AdftSum, '.', bandpassMedianFreq, AdftSum, '-');
 xlim([0,5000]); title(strcat(int2str(melFilterNum),' 次元に圧縮された振幅スペクトル'));
 subplot(2,2,4); plot(bandpassMedianFreq, AdftSum_log, '.', bandpassMedianFreq, AdftSum_log, '-');
 xlim([0,5000]); title(strcat(int2str(melFilterNum),' 次元に圧縮された対数振幅スペクトル'));
  • 結果は以下のようになります。
    filter19.png
  • メルスケールで等間隔な20次元に圧縮された対数振幅スペクトルに対して、離散コサイン変換(DCT) を行い、20次元のケプストラムに変換し、ケプストラムの低次成分（スペクトルの声道成分）12次元を取り出します。
    • 以下を実行 
       %コサイン変換
 cpst = 12;      % ケプストラム係数（低次成分何次元を取り出すか）
 AdftCpst = dct(AdftSum_log);
 AdftCpst_low = AdftCpst(1:cpst);
 figure(4); plot(AdftCpst, '.'); hold on; plot(AdftCpst_low, 'r.');
 xlabel('ケフレンシー'); ylabel('メル周波数ケプストラム係数');
    • 結果は以下のようになります（赤の部分が低次成分12次元）。*17
      filter20.png
↑

メルフィルタバンク解析（振幅スペクトルを分割するやり方） †

  • 音声波形に対してデジタルフィルタ（fir 関数）を適用するのではなく、振幅スペクトルや対数振幅スペクトルに直接フィルタ（ゲイン特性の理想応答のベクトル）をかけてもＯＫです。*18
    • この場合、「振幅スペクトルを求める」→「理想応答のメルフィルタバンクに振幅スペクトルを掛け合わせて、各帯域のスペクトルの和を求め*19、振幅スペクトルを20次元に圧縮する」→「対数をとって、声道・声帯成分の重ね合わせに変換」→「コサイン変換をしてケプストラムに変換」→「ケプストラムの低次12次元を取り出して声帯成分を除去」という順番でMFCCに変換します。*20
  • メルスケールの変換関数 mellog.m 、指定したベクトルの中で指定した値に一番近い値の番号を出力する関数 getNearNum.m、スペクトル解析のスクリプト calcSpectrum.m を同じディレクトリに入れた状態で、melFilterbankAnalysis を実行します。
  • 結果は以下のようになります。
    filter21.png
↑

自己相関関数 †

*1 青木直史,ディジタル・サウンド処理入門,CQ出版,2006 より引用
*2 梢 奇方, 島村 徹也, 高橋 淳一, 鈴木 誠史, "線形予測分析に基づくホルマント周波数抽出の雑音耐性の改善," 電気情報通信学会誌, Vol.J84-A, No.6, pp.745-758, 2001.
*3 Wikipedia より引用。以下の説明ではハニング窓を遣って説明しているところもありますが、特に特別な理由があるわけではありません。
*4 参考文献：MATLABマルチメディア信号処理〈下〉音声・画像・通信
*5 Auditory Toolbox マニュアル - mfcc を参照してください。
*6 参考文献：池原雅章, 島村徹也, "MATLABマルチメディア信号処理 上 ディジタル信号処理の基礎", 培風館, 2004.
*7 実例として、山野貴一郎, 伊藤克亘, スペクトル情報を用いたライフログ映像のシーン検出, 音声ドキュメント処理ワークショップ講演論文集, 2, pp.121-128, 2008. などがあります。
*8 バンドパスフィルタの設計手法は MATLAB 音声信号処理 fir1の利用例3：帯域通過フィルタ（北海道大 豊村先生）を参考にしています。
*9 バンドパスフィルタの設計手法は MATLAB 音声信号処理 fir1の利用例3：帯域通過フィルタ（北海道大 豊村先生）を参考にしています。
*10 ※MATLABコミュニティ octave も参考になります。
*11 「1/3オクターブバンドについて質問です。」、「1/3オクターブバンドについて」も参考にしました。
*12 バンドパスフィルタの設計手法は MATLAB 音声信号処理 fir2の利用(周波数応答の形状を設定)（北海道大 豊村先生）を参考にしています。
*13 このやり方だとサンプリング周波数の値によってスペクトルの最大周波数が変わり、MFCCの値も変わってしまう。サンプリング周波数ごとの最適なフィルタ数は要検討。
*14 参考：IT Text 音声認識システム, オーム社, p.14
*15 ここでは関数sumを使って、ベクトルの単純な和を求めていますが、これで正しいかどうか調べる必要あり！
*16 帯域フィルタバンク分析とは～与えられた波形をBPFを用いて対数的に等分して、それらの平均を出力とするものです。（帯域フィルタバンク分析 より引用）
*17 1番目の値だけ大きいのはなぜか？
*18 というか、こちらが一般的なMFCCのやり方のようです。
*19 ここでは関数sumを使って、ベクトルの単純な和を求めていますが、これで正しいかどうか調べる必要あり！
*20 参考：MFCCの計算方法、音響信号処理特論 音声処理における距離尺度（奈良先端大 猿渡先生）
添付ファイル: filemtlb_mfcc_4.png 4988件 [詳細] filemtlb_mfcc_3.png 5098件 [詳細] filecps_001.png 4599件 [詳細] filegetNearNum.m 4734件 [詳細] fileanalyzeNoize.m 5496件 [詳細] filea_pitch_praat.txt 3911件 [詳細] filelpc_01.png 6478件 [詳細] filea.wav 9978件 [詳細] filemtlb_mfcc_5.jpg 5834件 [詳細] filemtlb_mfcc_4.jpg 2414件 [詳細] filemtlb_mfcc_3.jpg 2603件 [詳細] filemtlb_mfcc_2.jpg 5509件 [詳細] filemtlb_mfcc_1.m 1840件 [詳細] filemtlb_mfcc_1.jpg 8731件 [詳細]