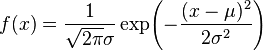R Note/統計/線形モデル
Last-modified: 2016-10-20 (木) 19:46:41
(一般)線形モデル : (General) Liner Model*1 †
- データ群が正規分布(Normal Distribution, または ガウス分布, Gaussian Distribution)に従う場合の統計解析*2
- データの測定誤差の分布は正規分布に従う
- 自然現象のさまざまなデータは正規分布する
- 平均値をμ、標準偏差をσとすると、以下の式であらわされる曲線が、正規分布
- 正規分布するデータ群のどの値が、どの程度の出現確率であるかは、正規分布表を使って求めることができる。
- Rで作ってみる:R Note/統計/確率分布/正規分布
- 線形モデルの注意点
- 全てのデータが正規分布にしたがうとは限らない
- 一般的な対応:ヒストグラムを書いてみて分布が左右対称・末広がりになっているかどうかチェックする
- 厳密な対応:事前にコルモゴロフ・スミルノフ検定などで正規性を検定する
- 正規分布でなかったときの対処
- 対数変換などをつかって正規分布に近づくよう前処理する(一般的な対処)
- 正規分布以外の分布に対応したモデル(一般化線形モデル)を使う
- 分布を仮定しないモデル(ノンパラメトリックモデル)を使う → ただし有意差は出にくい
- さらに詳細な議論を R Note/統計 で行なっています。
t検定 †
- 二つのデータ群(標本)について、それぞれのデータ群の平均に差(有意差)があるといえるかどうかを調べる手法。
- 前提条件
- 二つのデータ群がどちらも正規分布していること
- ニつのデータ群の分散が等しいこと
- わかりやすい例:役に立つ薬の情報~専門薬学>統計学>F検定(等分散の検定)
- F検定 で分散が等しいかどうかを調べる → 分散が等しいと仮定できない場合、ウェルチのt検定を使う。*3
- それぞれのデータ群が独立である(相関がない、対応がない = もう一方のデータ群の影響を受けない)こと
- 独立でない場合(両データで同じ被験者が参加しているなど) → 対応のあるt検定
- 一般に、対応を考慮したほうが有意差は出やすくなる。
分散分析(ANalysis Of VAriance, ANOVA)*4 †
- データ群が三つ以上ある場合、ニ群ずつそれぞれの組み合わせでt検定を行うのは適切ではない。
- 有意差がないのにあると誤判断される確率(危険率)が上がってしまう。
- 複数の群をまとめて検定するのが、分散分析(ANOVA)
- よりわかりやすい解説:ハンバーガー統計学にようこそ!(早稲田大向後先生) 6.2 分散分析とは
- 分析の目的やデータの種類に応じて、様々なANOVAがある。
- 多くの実験データの分析において、頻繁に使われる手法
- 分散分析の概要は 大村平, 実験計画と分散分析のはなし, 日科技連 および ハンバーガー統計学にようこそ! に詳しくまとめられています。詳細な配置条件及び分散分析結果の解釈・記述方法については 田中敏, 山際勇一郎, ユーザーのための教育・心理統計と実験計画法, 1992. がおすすめです。
- Analysis of Variance(浦島先生)も分かりやすい。
(対応のある/ない)一元配置分散分析 †
(対応のある/ない)二元配置分散分析 †
相関と回帰分析 †
- Rによるデータサイエンス、金明哲 著、森北出版、2007 に詳しい解説があります。
- 2つの変数間に相互依存関係があるかどうかの解析 → 相関分析
- 一方の変数の大小にともなってもう一方の値も変わるなら(例えば身長と体重)、「相互依存関係にある」といえます。
- 各データはそれぞれ、正規分布に従う誤差をもつと考える
- 1 に近いとき:正の相関がある
- -1 に近いとき:負の相関がある
- 0 のとき:相関はない(両変数は互いに独立)
- 2つの変数が相互依存関係にあるとき、2変数の関係を一次関数であらわす → (線形)単回帰分析*5
- 各データが正規分布に従う誤差をもつと考えて、最小二乗法に基づく式の推定を行っている
- わかりやすい詳細な解説:回帰分析(1)(早大阿部先生)
- MATLABで回帰分析:MATLAB Note/統計/回帰分析
- 類似手法の比較:Wikipedia 重回帰分析 関連する分析手法
- 各データが正規分布に従う誤差をもつと考えて、最小二乗法に基づく式の推定を行っている
- 2変数の関係をx次関数であらわす → x次回帰分析
- 変数が三つ以上のときの回帰分析 → (線形)重回帰分析
線形単回帰分析(説明変数が一つ) †
線形重回帰分析(説明変数が二つ以上) †
交互作用を考慮した重回帰分析(説明変数同士の影響を考慮) †
最適なモデル選択 †
(線形)混合(効果)モデル : Linear Mixed*6 Effect Model †
- 個人性や場所などの変量効果(ランダム要因)を考慮した上で除外できるモデル*7
- 固定モデル、無作為モデル、混合モデルとも呼ばれる*8
- 以下、動物行動学者のための一般化線形混合モデル:自習の手引き より引用
- ランダム要因:独立要因のひとつではあるが、その要因間の差に興味がない場合
- ランダム要因を入れることで、擬似反復pseudo-replicationを避けることができる
- ある個体から10個のデータが得られていて、他の個体からは5つのデータが得られている場合(データの独立性が保たれていない場合)でも、全部のデータ15個をプールして分析することができる
- 参考文献
- Mixed Effects Models Blog(理研 神長先生)
- 混合モデルを使って反復測定分散分析をする(理研 井関先生)
- 生態学のデータ解析 - ランダム効果とは?(久保拓弥先生)
- Linear Mixed Model (以下、混合モデル)の短い解説(北海道大 隅田先生)
- 一般化線形混合モデル入門の入門(名古屋大学 田村さん)
- R の統計パッケージ lme4 が提供している関数 lmer がよく使われる。
独立変数が一つかつ離散変数(一要因の混合効果分散分析) †
独立変数が一つかつ連続変数(混合効果単回帰分析) †
独立変数が複数(混合効果分散分析/重回帰分析/共分散分析) †
一般化(一般)線形モデル : Generalized Linear Model*9 †
- データ群が正規分布に従わない場合も含めた統計解析
- 参考文献:
- 観測されたパターンを説明する統計モデル(久保拓弥先生)
- 例題で考える一般化線形混合モデルの導入と計算(久保拓弥先生)
- GLM入門編1 一般化線形モデル
- ロジスティック回帰分析(大阪大鳥居さん)
- (一般)線形モデルと一般化線形モデルの違いについて:一般化線形モデルについて(北海道大 加藤先生)
- 以下は一般化線形モデルの一例です。
ロジスティック回帰分析 †
- 従属変数が離散かつ二値(二項分布)、独立変数が連続値
- 実例:R Note/音響解析データの統計解析/ロジスティック回帰分析
ロジスティック分散分析 †
- 従属変数が離散かつ二値(二項分布)、独立変数が離散値
ポアソン分散分析 †
- 従属変数が度数やカウントデータ(ポアソン分布)、独立変数が離散値
一般化(線形)混合(効果)モデル : Generalized Linear Mixed Effect Model †
- データ形状が正規分布に限定されず、かつランダム要因も考慮可能なモデル
- 実例:R Note/音響解析データの統計解析/ロジスティック混合効果モデル
階層ベイズ一般化線形モデル †
- 分布の種類以外にも、(最尤法で記述可能な)様々な前提条件を考慮可能なモデル
- 参考
- 関連
- ベイズ確率モデル
- 尤度は既知の分布を仮定するか、(任意の?)尤度式を指定する。確率密度関数はMCMC法によって求めるため既知の分布の制約を受けない。
- 事前分布は主観的に決めるか、既知の分布(正規分布)を仮定するか、分布形状を指定しない。階層型ベイズモデルでは観測データから事前分布の形状を求める。詳細は 階層ベイズモデル(北海道大 久保先生)を参照。
*1 GLMという略語は、一般線形モデルと、一般"化"線形モデルの両方を表す ため、ややこしいです。
*2 一般化線形モデルについて(北海道大 加藤先生)
*3 Rのt.test関数なら、自動的に分散を調べて適切なt検定を使ってくれる。
*4 http://www.ibaraki-kodomo.com/toukei/anova.html および ハンバーガー統計学にようこそ!(早稲田大向後先生) を参考にしています。
*5 Wikipedia - 線形回帰 より引用
*6 「混合モデル」の"mixed"と、「混合分布モデル」の"mixture"は違うものなので注意。前者はランダム要因の混合のこと。後者は確率分布の山が混合しているということ。
*7 ランダム要因になりうる様々な要因を混合モデルに入れて考慮することができる。制御要因とランダム要因に同一の要因を与えることもできるらしい。
*8 心理学のためのデータ解析テクニカルブック, 森敏昭, 吉田寿夫, 北大路書房 p.75-76
*9 一般線形モデル(General Linear Model, GLM または LM)はy=ax+bで表される線形モデルのうち、yが正規分布にしたがうもの全てをまとめたもの。一般化線形モデル(Generalized Linear Model, GLM)は、一般線形モデルをyが正規分布以外の既知の分布でも良いように一般化したもの(つまり、「一般化一般線形モデル」の略称)。階層ベイズ一般化線形モデルは、一般化線形モデルを階層ベイズモデルで表現してMCMCで解かせるもの。一般線形モデルについて や 一般化線形モデル (generalized linear model; GLM) を簡単に紹介するペイジ、一般化線形モデル入門の入門 を参照。