自己組織化マップの概要

Last-modified: 2013-02-27 (水) 04:08:32

自己組織化マップの概要 †

自己組織化マップ（Self-Organizing Maps, SOM）とは †

• 統計学的説明 ： 多くのパラメータを使うことで近似的にノンパラメトリックで非線形なPCA（主成分分析）を実現する手法*1
  • PCAとは … 多次元のデータを、できるだけ情報量を落とすことなく、低次元に要約する。
    • 例 : [数学の点, 国語の点, 理科の点, 社会の点] → [数学+理科の点, 国語+社会の点]*2
  • 非線形PCAとは … 非線形関数であっても推定可能、SOM や カーネル主成分分析 など。
    • 例 : 三角関数（データが原点を中心にした円弧上に存在する場合、x,yは偏角θの1次元で表現できる）*3
• 生理学的説明 ： 大脳感覚野の特徴地図が知覚経験によって形成されていく様子を説明したモデル（の、簡易版）*4
  • 網膜細胞の入力から、一次視覚野の方位選択性+眼優位性構造 を再現することができる。
• 応用的説明 ： マインドウエア総研 自己組織化マップとは？

理論 †

• SOMは入力層（入力データを与える層）、SOM層（競合層）からなる。
  • 入力層は R 個のノード（ニューロン）からなる。1つのノードは入力データの1次元（1つの特徴量）を表現することができる。すなわち、SOMには R 次元（ R 種類の特徴量）までの入力データを与えることができる。
  • SOM層は2次元または1次元にノードが配置された構造をもつ。ここでは M(縦軸方向のノード数) × N(横軸方向のノード数) = S 個のノードをもつとする。
    
    • 視覚に例えると、入力層が網膜のニューロン、SOM層が一次視覚野のニューロンに対応する。

• 入力層のノードは、ある時点でSOMに与えられる入力ベクトルを表現する。*5
  • SOMに与えられる入力ベクトル
    
    は、入力層のノード数と同じR次元で、絶対値1に規格化されている。*6
    

• ベクトルpの絶対値は、
  
  であるので、pの絶対値が1になるように規格化するには、pの各値をpの絶対値で割ればよい。
  • 例えば、ベクトル (1,0,1) を規格化すると、(1/√2,0,1/√2) になる。

• 続いて入力ベクトルの集合 P を定義する。
  • 学習を終えるまでにネットワークに与える全ての入力ベクトルの総数を Q 個として、それぞれの入力ベクトルが R次元のデータであるとすると、入力データの集合 P は 、以下のように表記できる。
    

• SOM層の各ノードは、参照ベクトル(reference vector)と呼ばれるR次元のベクトルを持つ。*7
  • i番目のノードの参照ベクトルは以下のように定義できる。
    
    
    • 参照ベクトルは、入力ベクトルと同じくR次元で、全て絶対値が1になるように規格化されている。*8
    • SOM層の各ノードは、入力層の全てのノードと、参照ベクトルμを介して結合している、ということ。
    • 参照ベクトルは、生理学的には神経細胞同士のシナプス結合の強さに相当する。ニューラルネットワークは、学習によってこの参照ベクトルを最適な値に調整するアルゴリズムであるといえる。

• SOM層は S 個のノードをもつので、各ノードについて参照ベクトルmを決めていくと、以下の行列Mが定義できる。
  
  • 初期状態では、各μの値はランダムに割り振るか、入力ベクトルの集合Pの中心値に設定しておくことが多い。

• 入力ベクトルpが入力層に与えられると、pに最も近い参照ベクトルを持つSOM層のノードが「勝者」となる。
  • ベクトル同士の「近さ」の判定方法は複数考えられるが、基本的なSOMではpとの内積が最も大きい参照ベクトルをもつノードを勝者であるとする。
  • すなわち、勝者をc番目のノードとすると、
    
    • mi・pの値が最大になるiの値がcになる、ということ。
    • 「・」はベクトルの内積を示す。なお、ベクトルxとyの内積は以下のようにして求める。
      
      
      のとき、
      
    • 入力ベクトルに対して、一つだけのノードが選択されるメカニズムは、生理学的には神経細胞同士の抑制性結合によって実現される。*9

• 勝者ノードが選ばれたら、SOM層上において、勝利ノードとその周辺のノードの学習がおこる。
  • SOMの学習は、参照ベクトルを入力ベクトルpに近づけることで実現される。

• ベクトルmi の値を、「(mi + hci × p)を絶対値1で規格化したベクトル」に置き換える、という意味。（「:=」は更新を示す）

• 上式の右辺の分子は、「ヘッブ学習」と呼ばれる、ニューラルネットワーク（神経細胞）の基本的な学習法則に対応している。参照ベクトルの学習の大きさを決める関数 hci は、SOMでは以下のように定義される。*10
  
  • αは学習の強さを表す1より小さな正の定数である。
  • exp記号以降は、正規分布（ガウス分布）をあらわす関数である。
  • riはSOM層のi番目のノードの2次元配列上での位置をあらわし、ri=(Ni,Mi)である。rcは勝利ノードの座標をあらわし、正規分布の平均値（山の中心）に対応する。また、||ri - rc|| は、「i番目のノードが勝利ノードからどれだけ離れているか」をあらわしている。
  • σは近傍の広がりを現す正の定数で、正規分布の標準偏差（山の裾野の広がりの大きさ）に対応する。
    

• 上式hciは、近傍関数またはKohonen学習関数とよばれ、「勝利ノードを頂点として、その周辺のノードを、α×正規分布の値にしたがって強化する」という意味。
  • ためしに、MATLABで正規分布を作ってみましょう。

        mu = 3.0;       %正規分布の平均値(中心座標、勝利ノードの番号)
        sigma = 2.0;    %正規分布の標準偏差(勝利ノードの周辺をどこまで強化するか)
        normalDist = zeros(100, 2)  %データを入力する配列を宣言
        for x = 0.1:0.1:10          %xは0.1から0.1ずつ10まで増えていく
            %xについて正規分布の値を求める
            y = exp( - (x - mu) .* (x - mu) / 2 * sigma .* sigma );
            normalDist( int16(x*10), : ) = [x y];   %x×10番目の配列にデータを代入
        end
        figure(1);
        plot(normalDist(:,1), normalDist(:,2));     %データをプロット
        xlabel('SOM層の座標'); ylabel('強化の強さ');

• SOMでは、入力ベクトルの集合Pからランダムに入力ベクトルpを与え、参照ベクトルの更新を繰り返すことで学習をすすめていく。
  • 学習の回数を「ステップ数」といいます。
  • 入力ベクトルの集合Pのデータ全てを1回ずつ与えたら、「1エポックの学習を行った」といいます。
  • αとσは定数でもよいが、学習の回数にしたがって減少させたほうがよりよい結果を得やすい*11
  • 「似た入力ベクトルに対しては、SOM層上の近い座標のニューロンが反応する」構造が自己組織的に形成されていきます。

• SOMの実行例は、こちら にあります。

• 信号空間内で頻繁に現れる領域は、ノード配列上で広い範囲にマップされる。
  • 入力の確率密度関数 p(x)と、参照ベクトルの確率密度関数 ρ(x)の間には、以下の関係がある。*12
    
  • 「A∝B」（AはBに比例する）
  • 上式が成り立つには、「ノード配列と入力がともに1次元である」「近傍のサイズが、ノード配列全体に対して十分小さい」「近傍の中に含まれるノードの数が十分小さい」という条件が必要

実装 †

• MATLABを使って、簡単なSOM（ヒモ状の内積型SOM）を再現してみよう。
• 縦方向のノード数 8 × 横方向のノード数 1 の、1次元のヒモ状のSOM層を考える。

  som_node = cell(8,1)

   som_node = 
       []
       []
       []
       []
       []
       []
       []
       []

• 将来、多次元のSOMを作ることも考えて、セル配列 で定義しています。

• 入力層は4つのノードからなる（=入力ベクトルが4次元）であるとする。すなわち、SOM層の8つのノードそれぞれが、入力層の4つのノードに対して重みをもつ。
  • 最初の重みの値は0～1までの間で、ランダムにする。

      for somNum = 1:1:length(som_node)
         som_node{somNum,1} = rand(1,4);
      end

    • 初期状態では、もう少しばらつきが小さいほうがいいかも
  • 格納された値を確認するには、

      for somNum = 1:1:length(som_node)
         disp( strcat('SOMのノード番号 : ', int2str(somNum), ',1') );
         disp( som_node{somNum,1} );
      end

    SOMのノード番号 :1,1
        0.3819    0.4322    0.0407    0.6870
    SOMのノード番号 :2,1
        0.8054    0.5061    0.1841    0.8513
    ...
    SOMのノード番号 :8,1
        0.5383    0.9785    0.2062    0.9239

    ※実行結果は毎回変わります。

• 8つのノードそれぞれについて、4つの重み値が定義された。

• 同じノード内で重みベクトルの内積が1絶対値が1になるように、値を正規化します。

    for somNum = 1:1:length(som_node)
        weight = som_node{somNum,1};
        scPrSom = sqrt( sum(weight.*weight) );  %正規化前の内積
        newWeight = weight / scPrSom;           %正規化後の内積
        som_node{somNum,1} = newWeight;         %重み値を書き換える
        disp( strcat('SOMのノード番号(正規化後) : ', int2str(somNum), ',1') );
        disp( som_node{somNum,1} );
    end
  }
  >
   SOMのノード番号(正規化後) :1,1
       0.4253    0.4813    0.0453    0.7651
   SOMのノード番号(正規化後) :2,1
       0.6245    0.3924    0.1427    0.6601
   ...
   SOMのノード番号(正規化後) :8,1
       0.3677    0.6684    0.1408    0.6311
  &color(red){※実行結果は毎回変わります。};
  
  ---これで、ネットワークの初期化は完了。
  --初期状態の%%重み値%%&color(red){参照ベクトル};を視覚化して確認してみましょう。
  #geshi(matlab){{
    data = zeros(9,4);
    for somNum = 1:1:length(som_node)
          data(somNum,:) = som_node{somNum,1};
    end
    countNode = (1:1:length(som_node))';
    surf( [data countNode] );   %色つき立体グラフで表示
    view(2);                    %平面表示
    xlabel('入力層ノードの番号'); ylabel('SOM層ノードの番号')

• 関数surfは一番端の行がプロットされないので、データの行数を9(8ノード+1)にしています。

• 続いて、入力ベクトルの集合（4次元の入力ベクトル×150データ）を作ってみよう。
  • 4次元なので、Fisherのアヤメの測定データを使います。
  • これは、以下のように、3種類のアヤメ150サンプルに対して、がくの長さと幅、花弁の長さと幅を測定したものです。

    花のID	花の種類	がくの長さ	がくの幅	花弁の長さ	花弁の幅
    1	1	5.1	3.5	1.4	0.2
    2	1	4.9	3	1.4	0.2
    ...	...	...	...	...	...
    150	3	5.9	3	5.1	1.8

• 例えば、ここを参考にアヤメのデータをダウンロードして、以下を実行

    inputdata = csvread('アヤメのデータ.csv',1,2)

  inputdata =
    5.1000    3.5000    1.4000    0.2000
    4.9000    3.0000    1.4000    0.2000
  ...
    5.9000    3.0000    5.1000    1.8000

• 引数の(1,2)は、「縦は1行目から最後まで読み込む（最初のヘッダ情報を読み込まない）、横は2列目から最後まで読み込む（花のIDと種類を読み込まない）」という意味。
• 注意：基本的に、MATLABでは「0行目」「0列目」という言い方はせずに1から数え始めるのですが、ここだけは0=最初の行の番号、という扱いです。

• このままでは、次元（特徴量）ごとに数値の最大・最小値が違っていて不便なので、各特徴量が0～1の範囲になるように、正規化します。

    inputVector = zeros(150,4);
    %次元（特徴量）ごとに処理する
    for inpNum = 1:1:4
        %まずは、各データからその次元の最小値を引く（0から始まるデータにする）
        zeroStartData = inputdata(:,inpNum) - min( inputdata(:,inpNum) ) ;
        %続いて、各データをその次元の最大値で割る（1で終わるデータにする）
        inputVector(:,inpNum) = zeroStartData / max(zeroStartData);
    end
    inputVector

  inputVector =
     0.2222    0.6250    0.0678    0.0417
     0.1667    0.4167    0.0678    0.0417
  ...
     0.4444    0.4167    0.6949    0.7083

• これで、4列（次元、特徴量） × 150行で 0～1 の、入力ベクトルの集合 inputVector ができました。
• 入力ベクトルも内積が1になるよう正規化する必要あり!!

• ネットワークの学習を行います。
  • inputVector の 1行目を入力層に与えます。

      input_node = inputVector(1,:)

    input_node =
       0.2222    0.6250    0.0678    0.0417

• SOM層の各ノードの参照ベクトルと入力ベクトルを掛け合わせます。

    weightInputVector = zeros(8,4);  %掛け合わせた値を代入する変数を宣言
    for somNum = 1:1:length(som_node)
       weightInputVector(somNum,:) = som_node{somNum,1} .* input_node;
       disp( strcat('SOMのノード番号 : ', int2str(somNum), ',1') );
       disp( weightInputVector(somNum,:) );
    end

  SOMのノード番号 :1,1
      0.0945    0.3008    0.0031    0.0319
  SOMのノード番号 :2,1
      0.1388    0.2452    0.0097    0.0275
  ...
  SOMのノード番号 :8,1
      0.0817    0.4177    0.0095    0.0263

  ※実行結果は毎回変わります。

• 更新された各ノードの重み4次元を足し合わせた結果、もっとも大きな値を持っていたノードが、「勝利ノード」に選ばれます。

    sumSomNode = zeros(8,1);   % 各ノードの合計値を代入する変数を宣言
    for somNum = 1:1:length(som_node)
       sumSomNode(somNum) = sum( weightInputVector(somNum,:) );
    end
    %もっとも合計値が大きかったノードの番号を取得する
    winnerSomNumber = find( sumSomNode == max(sumSomNode) );
    disp( strcat('勝利ノードの番号 : ', int2str(winnerSomNumber)) );

  勝利ノードの番号 :3

  ※実行結果は毎回変わります。

• 勝利ノードとその周辺のノードの重みを、入力ベクトルに近づけるように更新します。
  • 強化関数を定義します。

      somNum = [1:1:length(som_node)];
      learningRate = 0.1;     %学習率(1回の学習で、入力ベクトルにどれだけ近づけるか)
      mu = winnerSomNumber;   %正規分布の平均値(中心座標、勝利ノードの番号)
      sigma = 2.0;            %正規分布の標準偏差(勝利ノードの周辺をどこまで強化するか)
      reinforcement = learningRate ...
           * exp( (-(somNum - mu) .* (somNum - mu)) / 2 * sigma .* sigma );
      figure(1);
      plot(reinforcement); xlabel('SOMノードの番号'); ylabel('強化の割合');

  • learningRate = α に対応
  • 強化の度合いの関数は、勝利ノードを中心した正規分布とします。
    

• 強化関数は以下のようになります（※平均値=勝利ノードの番号は毎回変わります）。
  

• 勝利ノードを中心として、標準偏差で指定した値のノードまでが強化の対象になります。
• 強化関数にしたがって、重み値を入力ベクトルに近づけます。

    for somNum = 1:1:length(som_node)
        weight = som_node{somNum,1};
        newWeight = weight + ((input_node - weight) * reinforcement(somNum));
        som_node{somNum,1} = newWeight;         %重み値を書き換える
        disp( strcat('SOMのノード番号(更新後) : ', int2str(somNum), ',1') );
        disp( som_node{somNum,1} );
    end

  SOMのノード番号(更新後) :1,1
      0.4253    0.4813    0.0453    0.7651
  SOMのノード番号(更新後) :2,1
      0.6190    0.3955    0.1417    0.6517
  ...
  SOMのノード番号(更新後) :8,1
      0.3677    0.6684    0.1408    0.6311

  ※実行結果は毎回変わります。

• 同じノード内で参照ベクトルの内積が1になるように、値を正規化します。

    for somNum = 1:1:length(som_node)
        weight = som_node{somNum,1};
        scPrSom = sqrt( sum(weight.*weight) );  %正規化前の内積
        newWeight = weight / scPrSom;           %正規化後の内積
        som_node{somNum,1} = newWeight;         %重み値を書き換える
    end

• これで、一回の学習の処理が終了しました。

• 同様にして、入力ベクトルの集合からランダムに各行を取り出しながら、十分な回数の学習を行います。

    learningSteps = 1000;       %学習の回数を決める
    for step = 1:1:learningSteps
         disp(strcat('leanrnig steps... ', int2str(step)));
         %今回使う入力ベクトルの番号をランダムに選択する
         input_node_num = ceil(rand() * length(inputVector));
         input_node = inputVector(input_node_num,:);
         %勝利ノードを計算する
         weightInputVector = zeros(8,4);  %掛け合わせた値を代入する変数を宣言
         sumSomNode = zeros(8,1);   % 各ノードの合計値を代入する変数を宣言
         for somNum = 1:1:length(som_node)
             weightInputVector(somNum,:) = som_node{somNum,1} .* input_node;
             sumSomNode(somNum) = sum( weightInputVector(somNum,:) );
         end
         winnerSomNumber = find( sumSomNode == max(sumSomNode) );
         %重み値を更新する
         somNum = [1:1:length(som_node)];
         learningRate = 0.1;     %学習率(1回の学習で、入力ベクトルにどれだけ近づけるか)
         u = winnerSomNumber;    %正規分布の平均値(中心座標、勝利ノードの番号)
         sigma = 2.0;            %正規分布の標準偏差(勝利ノードの周辺をどこまで強化するか)
         reinforcement = learningRate ...
              * exp( (-(somNum - u) .* (somNum - u)) / 2 * sigma .* sigma );
         for somNum = 1:1:length(som_node)
                weight = som_node{somNum,1};
                newWeight = weight + ((input_node - weight) * reinforcement(somNum));
                som_node{somNum,1} = newWeight;         %重み値を書き換える
         end
         %重み値を正規化する
         for somNum = 1:1:length(som_node)
                weight = som_node{somNum,1};
                scPrSom = sqrt( sum(weight.*weight) );  %正規化前の内積
                newWeight = weight / scPrSom;           %正規化後の内積
                som_node{somNum,1} = newWeight;         %重み値を書き換える
         end
     end

• 学習が終わった後の重み値は、以下のようにして確認します。

    for somNum = 1:1:length(som_node)
        disp( strcat('SOMのノード番号(学習後) : ', int2str(somNum), ',1') );
        disp( som_node{somNum,1} );
    end

  SOMのノード番号(学習後) :1,1
      0.4330    0.7556    0.0967    0.4819
  SOMのノード番号(学習後) :2,1
      0.3773    0.9137    0.1103    0.1035
  ...
  SOMのノード番号(学習後) :8,1
      0.3842    0.3107    0.5992    0.6300

  ※実行結果は毎回変わります。

• これで、ネットワークの学習は終了です。

• クローズドテストで正解率を求めてみます。
  • 入力データファイルの2列目(アヤメの種類)を読み込みます。

     targetdata = csvread('iris_JMP.csv',1,0);
     targetdata = targetdata(:,2);     %2列目を取得

    • アヤメの種類データは1,2,3の数値で表現されています。
  • 正解率の求め方はいろいろ考えられますが、ここでは「同じ種類のデータを提示したときの勝利ノードの番号」を求め、「データ密度ヒストグラム」で表示してみます。

      %入力データの種類ごとにヒストグラムを作る
      dataHistgram = [];
      %アヤメの種類:1 の勝利ノードを格納するベクトル
      evalWinnerSomNumber_1 = [];
      %アヤメの種類:2 の勝利ノードを格納するベクトル
      evalWinnerSomNumber_2 = [];
      %アヤメの種類:3 の勝利ノードを格納するベクトル
      evalWinnerSomNumber_3 = [];
      %勝利ノードを計算する
      for evalNum = 1:1:length(inputVector)
          input_node = inputVector(evalNum,:);
          %勝利ノードを計算する
          weightInputVector = zeros(8,4);  %掛け合わせた値を代入する変数を宣言
          sumSomNode = zeros(8,1);   % 各ノードの合計値を代入する変数を宣言
          for somNum = 1:1:length(som_node)
              weightInputVector(somNum,:) = som_node{somNum,1} .* input_node;
              sumSomNode(somNum) = sum( weightInputVector(somNum,:) );
          end
          winnerSomNumber = find( sumSomNode == max(sumSomNode) );
          if(targetdata(evalNum)==1)
              evalWinnerSomNumber_1 = [evalWinnerSomNumber_1 ; winnerSomNumber];
          elseif(targetdata(evalNum)==2)
              evalWinnerSomNumber_2 = [evalWinnerSomNumber_2 ; winnerSomNumber];
          elseif(targetdata(evalNum)==3)
              evalWinnerSomNumber_3 = [evalWinnerSomNumber_3 ; winnerSomNumber];
          end
      end
      %頻度分布を計算
      dataHistgram = [ ...
          hist(evalWinnerSomNumber_1, [1:1:length(som_node)]) ; ...
          hist(evalWinnerSomNumber_2, [1:1:length(som_node)]) ; ...
          hist(evalWinnerSomNumber_3, [1:1:length(som_node)]) ];
      %ヒストグラムをプロット
      figure(2);
      bar(dataHistgram');
      xlabel('SOMのノード番号'); ylabel('頻度(勝利ノードに選ばれた数)'); 
      legend('1', '2', '3');

• 結果は以下のようになります（※実行結果は毎回変わります）。
  
  • カテゴリー1のアヤメを代表するSOMノードは2番（とその周辺）、カテゴリー2を代表するSOMノードは5番、カテゴリー3を代表するSOMノードは6番と判断できます。
  • ただし、カテゴリー1に比べて、カテゴリー2と3の弁別は十分にできていないことも分かります。入力データの特徴量に差がない可能性、学習の回数が足りない可能性などが考えられます。

【拡張】カテゴリの数を推定する †

(寺島，1996)による方法 †

• 母音体系の獲得過程をシミュレーションする上で、従来のSOMモデルでは解決が困難な問題がある。
• 例として、分散が等しく平均が異なる正規分布をSOMによって分類する場合を考える。

• 上図に示したのはクラスタごとに平均の異なる、3種類の（3クラスタの）2次元正規分布

• ここで、分類したいクラスタ（カテゴリ）数が既知の場合を考える。
• SOMの学習では、「分類したいクラスタ数 = S（出力層のノード数）」とする手法が一般的である。
  • 値はランダムな順番でSOMに提示していくとする。

• 上図は学習結果の例である（S = 1×3 = 3ノードの1次元SOM）。
• それぞれ、ほぼ正しいクラスタ境界を学習できている。

• 次に、クラスタ数が不明の場合を考える。
  • 母音数は言語によって異なり、乳児は母国語に応じた母音数を学習しているため、こちらの方が言語獲得モデルとして妥当な問題であると思われる。
  • 入力がどのような分布をとるか不明で、何種類のクラスタに分類できるのかも不明の場合は、SOMのニューロンの数は十分に多くとる必要がある。

• SOMによる学習の結果を示す（S = 1×6 = 6ノードの1次元SOM）。

• SOMでは、カテゴリ間の境界付近にニューロンが割り当てられ独立したカテゴリになる
  • ヒトの範疇化知覚を再現できているとはいえない。
  • 学習結果をもとに、類似したカテゴリを同一のカテゴリに統合して扱えるよう、モデルを拡張する必要がある

• ニューロンが1列に配置された1次元SOM について、以下のような有効な手法が提案されている*13

1. 学習を終えたSOM にテストデータセットを提示し、SOMのそれぞれのノード（ニューロン）が何回勝利ノードになったかを調べ、入力データのカテゴリ集積度を表すヒストグラムを作る。
2. ヒストグラムのピークピッキングを行い、カテゴリの中心となるノードを求める。
3. カテゴリ中心以外のノードの重みを0にして、入力データとの対応関係を再計算する。

• 上記の学習結果（S = 1×6 = 6ノードの1次元SOM）に対して、この手法を適用後のSOMの例を示す。

• SOMの学習結果のカテゴリ集積度を示すヒストグラム
  
  • カテゴリ集積度をみると、①④⑥番のノードがカテゴリ中心になっている

• 2,3,5番のSOMのノードの重みをゼロにして、各データがどの勝利ノードに対応付けられるかを再計算
  

• 再計算によってカテゴリが統合され、3つの正規分布を抽出できている

• 要検討事項
  • SOMのノード数が正解のカテゴリ数に対して多くなると、ピークピッキングがうまくいかない。
    • → ヒストグラムの曲線の平滑化が必要

• データ密度ヒストグラムを用いたクラスタ分類法（寺島,1996） のデモ
  • 以下のプログラムは、MATLAB Neural Network Toolbox の SOM を拡張して使用しています。
  • 入力の数のみによる判定（ L = V ）
    • 20110729_useTerashimaMethod.zip を解凍したディレクトリで RUN_terashimaMethod1.m を実行して下さい。
  • 入力の数＋重みによる判定（ L = V / dM ）
    • 20110729_useTerashimaMethod.zip を解凍したディレクトリで RUN_terashimaMethod2.m を実行して下さい。
    • 両端のノードの、（すなわち存在しない）隣接ノードの重みをどうとるかによって、両端が山になるか、谷になるかが変わる。

(加藤，2009)による(寺島，1996)の拡張 †

• (寺島，1996)の方法で獲得したカテゴリーをさらに正確に統合する手法が提案されている*14
  • 獲得したカテゴリーの隣あう各ペアについて、「統合した一混合GMM」と「別々のニ混合GMM」のどちらが良いか、AICを使って評価している。
  • AICとBIC（ベイズ情報量規準）を比較、AICの方が高精度だった
• サンプルプログラム RUN_TerashimaAndKatoMethod.m
  • そこそこの頻度で、カテゴリー数の推定がうまくいかない場合がある（数が多くなる*15）。
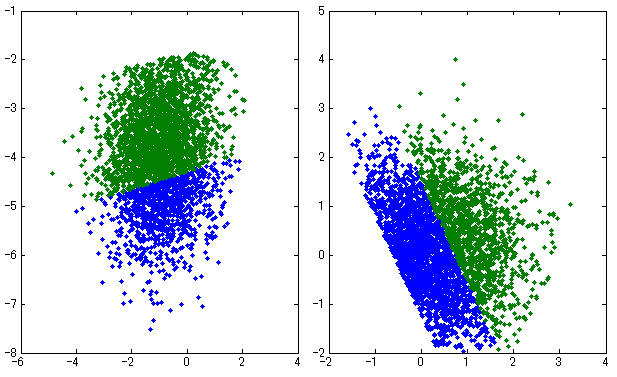
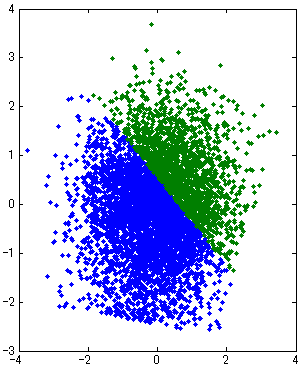
    • 例えば以下の場合、AIC, BICどちらも、誤って2クラスタに分類してしまった。なお、青と緑の分布は隣り合う各SOMノードに対応付けられた入力データを示す。この二つの分布を足しあわせた分布を最もよく説明するのは1混合モデルか、2混合モデルかを調べた。
      
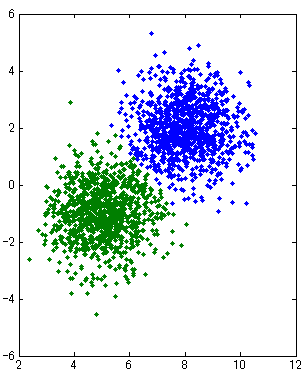
    • 以下の場合は両基準ともに正しく1クラスタに分類できた。
      
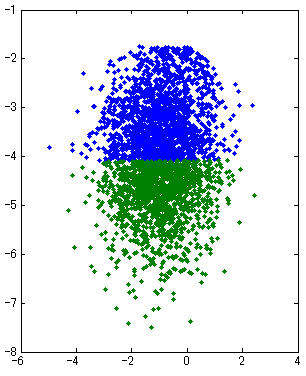
    • 以下の場合は、AIC, BICどちらも、誤って1クラスタに分類してしまった。
      
    • 以下はAICは誤って2クラスタに分類してしまったが、BICは正しく1クラスに分類した。今回の実験ではAICよりBICのほうがうまくいくようだった。
      
    • この手法によって取り出される分布は正規分布ではなく、分布のすそが削れている。それがAICの結果に影響していると思われる（BICは分布の重複と、それによる分布のすその欠損にある程度頑健であるようだ）。 → 検証用 testGMMandAIC.m testGMMandAIC_R.txt

検索

AND検索 OR検索  

更新履歴

最新の20件

edit
限定版