R Note/統計

Last-modified: 2016-10-20 (木) 19:54:55

R による統計解析 †

導入 †

変数の尺度（データ水準）*1 †

• データは４種類に分類可能で、それぞれ使用できる統計手法（統計量*2）が異なる
  • 名義尺度 の統計量 ： 各ケースの数、計数、頻度、最頻値、連関係数*3
    • 質的データ、カテゴリカルデータとも呼ばれる。データは度数集計表によってあらわされる。*4
  • 順序尺度 の統計量 ： 上に加えて、中央値、パーセンタイル*5
    • 順位尺度は間隔をもたないので、データ自体は数値であるが四則演算は成立しない。平均を求めることさえ無意味。その反面、正規分布を前提にしない・極端値に強い・少数データを扱えるといった強みがある。*6
  • 間隔尺度 の統計量 ： 上に加えて、平均値、標準偏差、順位相関係数、積率相関係数*7
    • 例えばデータが「クラスの各員の得点（間隔尺度）」であれば、平均値に統計的な意味があります。しかし「クラスの各員の得点の順位（順序尺度）」は、平均値には意味がなく、中央値もしくは最頻値が妥当です。*8
  • 比例尺度 の統計量 ： 上に加えて、変動係数*9

• 離散変数（カテゴリカル変数）と連続変数という分け方もある。
  • 名義尺度と順序尺度は離散変数。間隔尺度は離散・連続変数両方あり*10、比例尺度は連続変数。

• 平均値が統計量として意味を持つには（平均値 = その分布の代表値として妥当、となるためには）、「観測された変数の母集団が連続分布（かつ、正規分布）である」という前提が満たされていないといけない！
  • 例：バーに入ってきたビル・ゲイツ　→　分布にゆがみが有る場合、平均値が代表値として妥当ではなくなる
  • すなわち、離散データ、または正規分布でない連続データの解析に平均値（＋平均値に基づいた検定手法）を使うのは、注意が必要!*11
  • 順序尺度に対して平均値を使うための条件（東北大田中先生）　→　「正規分布する連続データから、一定・等間隔の尺度で抽出した」といえる離散データであれば、順序尺度と同等の統計をつかってもいい、ということのようです。ただし、厳密には避けるべきだと思われます。

平均と標準偏差*12 †

• 平均（Mean）は、データの値を全て足して、データの個数で割ったもの
  • n個のグループの値が
    
    のとき、
    

• 標準偏差（Standard Deviation）は、データの集合が平均値からどれだけばらけているかを示す値
  • n個のグループの値が
    
    のとき、標準偏差は
    
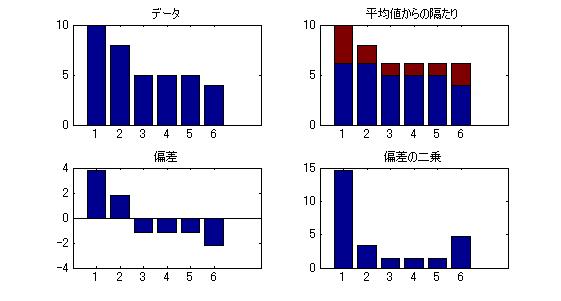
    • 偏差（Deviation）は、ある値の平均値からの隔たり
      
    • 偏差の平均はゼロになってしまう。そこで、「偏差の二乗」の平均をとってルートをかけたものが標準偏差

• 分散（Variance）は、標準偏差の二乗（ルートをかける前段階、数学的に扱いやすい）
  

データの分布とヒストグラム*13 †

• あるデータ集合の性質を調べる場合、平均と分散だけでなく、分布も重要である。
• それぞれの値が何回出現したかを示すグラフを、ヒストグラムという。
  • 下図の上は [3 3 3 3 3 4 4 4 5 5 5 6]　下は [2 3 3 4 4 4 4 4 4 5 5 6] のヒストグラム（このデータは、「統計のはなし（大村平著、日科技連）」より引用したものです）。どちらも平均・分散は同じ。

    hist(c(3,3,3,3,3,4,4,4,5,5,5,6), breaks = c(1,2,3,4,5,6), freq = TRUE)

    hist(c(2,3,3,4,4,4,4,4,4,5,5,6), breaks = c(1,2,3,4,5,6), freq = TRUE)

• ヒストグラムの縦軸を出現確率（データ全体に対して、その値が出現した割合）にしたものを、確率分布（probability distribution）という。縦軸の値を合計すると、必ず1になる。

  hist(c(3,3,3,3,3,4,4,4,5,5,5,6), breaks = c(1,2,3,4,5,6), freq = FALSE)

  hist(c(2,3,3,4,4,4,4,4,4,5,5,6), breaks = c(1,2,3,4,5,6), freq = FALSE)

• データが連続的な値であれば（小数のデータがあるなら）、確率分布も連続値（曲線）になる
  • これを確率密度関数（probability density function, p.d.f.）という。
  • 詳しくはR Note/統計/確率分布を参照して下さい。

• 離散変数と連続変数では、確率密度関数のグラフの意味が異なる
  • なぜか？ → 分布に上限、下限がある + 片方のカテゴリの出現確率が大きいと、分布が歪む*14
  • 詳細な議論：確率と統計（静岡理工科大 菅沼先生）
  • 正規分布を仮定できないので、離散変数はそのままでは平均値（＋それに基づいた統計）を使えない!

• イェーツの補正：度数で表されるような離散型分布を、カイ二乗分布や正規分布などの連続型分布に近似させて統計的検定を行おうとするときに用いる修正手続き。検出力は低下するが、より正確な検定が可能になる。*15

• 統計解析を行う前に、ヒストグラムを見てデータの分布を検討することが重要。
  • 要因と水準（実験条件）ごとにプロットした分布の形状が多峰性になっていた場合、実験条件の再検討が必要。
  • 分布の形状が左右対称でない（正規分布でない）場合、正規分布に近づけるように変換する必要がある
  • 外れ値（極端値、データ全体の分布から大きく外れて孤立しているような値）*16がある場合は、事前に外れ値を除外するか、順位尺度のデータとして扱う必要がある*17

パラメトリックとノンパラメトリックな分析法 †

• パラメトリックな分析法
  • 母数，つまり母集団の分布に関する何らかの仮定をおいた手法*18（中澤先生）
    • 例えば線形モデルでは 正規分布 を仮定する。
    • 一般化線形モデルでは 正規分布を含む様々な分布 を仮定する。
  • しかし，実際には正規分布にしたがっていない場合もある。この場合の戦略としては，(1) 対数正規分布とかガンマ分布のような別な分布を考える，(2) 正規分布に近づくような変換を施す，といったことが考えられるが，真の分布がわかっていないためにうまく行くとは限らない。そこで，ヒストグラムを描いてみて，どうも正規分布ではなさそうだと思ったら，分布によらない方法を試してみるというのも一案である。*19（中澤先生）

• どちらにしろ、データの分布が特定できて、適切な手法が使えるなら、ノンパラメトリックよりパラメトリックな手法の方がよい（有意差が出やすい）。データの分布が既知のどの分布と一致しているかを検定するには、コルモゴロフ＝スミルノフ検定（KS 検定）などを使う。

• ノンパラメトリックな分析法
  • 「データが何らかの分布をとる」といった仮定をしない統計手法。*20
    • 仮定がない分、上述の手法に比べると説明力は落ちる。したがって上述のモデルが使えない時に使うべき。
  • 「母数を仮定しない」とは言っても，連続分布であることだけは仮定する。*21（中澤先生）
  • ノンパラメトリック検定（木村先生）によれば、「ノンパラメトリック検定とは？ - 母集団分布に関して特定の仮定をおかない、名義尺度や順序尺度のデータ処理ができる」とある。
  • 統計的検定マニュアル には以下の記述。

    ノンパラメトリック検定：

    　２群の比較に中央値を用いて検定する。

    　そのためデータ分布を仮定せず離散値データ（とびとびの値）でもよい。

    　ただしデータが正規分布しているときは判定が厳しすぎる場合もある。

• データの統計処理（粟飯原先生） によれば、

  逆にノンパラメトリック検定を行うべき場合は

  １）明らかに正規分布でないとき。（逆数や対数をとって変数変換を行ったりする方法がある）

  ２）データの分散が群によって一様でないとき。

  ３）測定の尺度が間隔尺度でないとき。

  ４）分布の端で測定値が途切れているとき。測定感度以下のデータのあるとき。

• Wikipediaによれば、「中心極限定理によると、母集団の分布が正規分布に従わないと考えられる少数の標本では、標本平均が正規分布から遠く離れる。そのためt検定などを使うことが出来ず、ノンパラメトリックが数少ない分析手法となってしまう。」*22

統計手法の選択 †

• 条件間の代表値に意味のある差があるかどうかを調べたいとき：有意差の検定
• ある変数とある変数の間の関係性を調べたいとき：相関と回帰の分析
  • 何らかの真のモデルがあることを前提として、その真のモデルに最も近似するモデルを標本データから求める*23

• 以下の分類は、田中敏, 山際勇一郎, ユーザーのための教育・心理統計と実験計画法 : 方法の理解から論文の書き方まで, 1992． および パラメトリックな手法とノンパラメトリックな手法（群馬大青木先生）を参考にしました。

有意差の検定 †

• 比較するデータの種類が間隔尺度および比率尺度である
  • データが連続変数で、正規分布にしたがう*24
    • 2条件の比較である

      対応のないt検定 - 標準偏差が等しい

      対応のあるt検定 - 標準偏差が等しい、データに対応がある

      ウェルチのt検定 - 標準偏差が等しくない*25

• 複数条件の比較である*26

  分散分析 - 標準偏差が等しい、または等しくない*27

  クラスカル・ウォリス検定 - 標準偏差が等しくない

• データが連続変数で、正規分布にしたがわない

  順序尺度・名義尺度のデータとして扱う

  正規分布に変換して分散分析*28

• データが離散変数である

  クラスカル・ウォリス検定*29

  フリードマン検定 - データに対応がある

• 比較するデータの種類が順序尺度である
  • 2条件の比較である

    メディアン検定

    符号検定

    順位相関分析

• 複数条件の（交互作用の）比較は困難

• 比較するデータの種類が名義尺度である
  • 2条件の比較である

    直接確率計算

    カイ二乗検定

    連関係数分析（相関分析の離散変数版）

• 複数条件の比較である

  対数線型分析

相関と回帰の分析 †

• 用語
  • (Response / Dependent / Criterion)(Variable / Factor / Effect), または (応答/従属/基準)(変数/要因/因子/効果) : Xによって変化する「結果」の要因 Y, 1次元の連続量または離散量
  • (Fixed / Independent / Explanatory)(Variable / Factor / Effect), または (固定/独立/説明)(変数/要因/因子/効果) : 検証したい要因 X, 任意の次元の連続量または離散量
  • Random (Variable / Factor / Effect), または ランダム (変数/要因/因子/効果) : 独立要因のひとつではあるが、その要因間の差に興味がない場合

• 比較するデータの種類が間隔尺度および比率尺度である
  • データが連続変数で、正規分布にしたがう
    • 2条件の比較である

      散布図を書き、相関係数の有意性検定と単回帰分析

• 複数条件の比較である

  因子分析 - 従属変数-独立変数間の予測関係なし

  重回帰分析 - 従属変数-独立変数間の予測関係あり、相関なし

  交互作用を考慮した重回帰分析 - 従属変数-独立変数間の予測関係あり、相関あり

  線形混合モデル - 従属変数-独立変数間の予測関係あり、相関なし、ランダム変数あり

• データが連続変数で、正規分布にしたがわない

  順序尺度・名義尺度のデータとして扱う

  正規分布に変換して単/重回帰分析

  分布形状を指定して一般化線形モデル

• 比較するデータの種類が順序尺度である
  • 2条件の比較である

    順位相関分析

• 複数条件の（交互作用の）比較は困難

• 比較するデータの種類が名義尺度である
  • 2条件の比較である

    連関係数分析

• 複数条件の比較である

  対数線型分析

実例 †

• R Note/音響解析データの統計解析

検索

AND検索 OR検索  

更新履歴

最新の20件

edit
限定版