MATLAB Note/統計/確率分布

確率分布（確率密度関数） †

• 確率分布の特性と分類に関して、さまざまな確率分布（滋賀大中川先生） に総合的な解説があります。
• 以下、Statistics Toolbox の関数を使用します。
  • 参考：Statistics Toolbox でサポートされている確率分布
  • Rでも同じことができるはずです。R Note/統計/確率分布 を参照して下さい。

連続変数（Continuous variable） †

• 連続的に変化する値の出現頻度を扱う分布。
  • 【引用】 （略）棒が倒れる方向 X は、0 から 360°の間の任意の値を取ることができます。このような分布を連続型分布といいます。（略）ここで注意してもらいたいのは、離散型分布の確率関数とは異なり、確率密度関数 f(x) は、X が 値 x を取るときの確率を表しているわけではないことです。（略）なぜなら、倒れたときの角度がある特定の値に完全に一致する確率は限りなく 0 に近いからです。*1
  • 【引用】連続変数の分布では面積が重要。例えばX=aからX=bまでのx軸と確率密度曲線に囲まれた領域の面積 S は、Xの値が a から b の間に入る確率を意味する*2

正規分布（Normal distribution）、ガウス分布（Gaussian distribution） †

• 正規分布 - Wikipedia
  • 平均μ、標準偏差σから求まる
  • 左右対称、多くのデータが正規分布に従う
  • データの平均値の集合は、元のデータの分布の種類によらず正規分布になる（中心極限定理による）
  • HMM音響モデル の各状態における各音響特徴は、混合正規分布に従うことを仮定している。
  • 適当な区間の外側を0にすることで窓関数としても用いられる（？）

• μ = 0, σ = 1 の正規分布（標準正規分布）を作ってみます。
  • まずは以下を実行します。

    %パラメータの宣言
    mu = 0;
    sigma = 1;

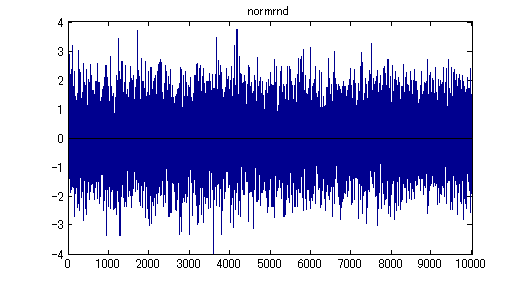
  • この分布に従う乱数を10000個(10000×1の配列で)作るには、関数 normrnd を使います。

    data = normrnd(mu, sigma, [10000 1]);                       % 乱数生成
    bar(data); xlim([0,10000]); title('normrnd');               % プロット

    
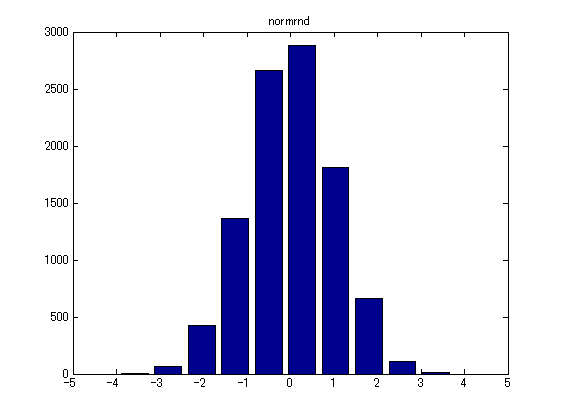
  • ヒストグラムで書いてみます。

    [histdata, position] = hist(data);                          % ヒストグラム
    bar(position, histdata); xlim([-5,5]); title('normrnd');    % プロット

    
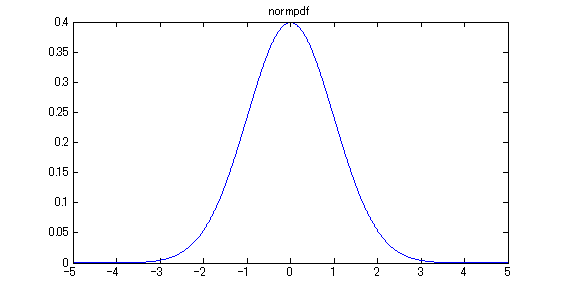
  • ヒストグラムの頂点を結んだ線が確率密度曲線（の近似）になります。より厳密な正規分布の確率密度曲線は、関数 normpdf でプロットできます。ここでは x座標 -5 ～ 5 までの区間（0.01刻み）で関数生成＆プロットしてみます。

    linescale = [-5:0.01:5];                                    % x座標のスケール
    pdfdata = normpdf(linescale, mu, sigma);                    % 確率密度関数生成
    plot(linescale, pdfdata); xlim([-5,5]); title('normpdf');   % プロット

    
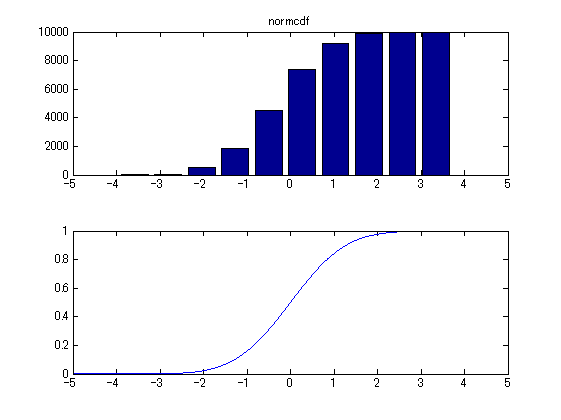
  • ヒストグラムの各バーを、x座標の小さいものから順に足しあわせてプロットしていけば累積密度曲線（の近似）になります。より厳密な正規分布の累積密度曲線は、関数 normcdf でプロットできます。

    histsum = cumsum(histdata);                                 % ヒストグラムの累積和
    cdfdata = normcdf(linescale, mu, sigma);                    % 累積密度関数生成
    subplot(2,1,1); bar(position, histsum); xlim([-5,5]); title('normcdf');
    subplot(2,1,2); plot(linescale, cdfdata); xlim([-5,5]);     % プロット

    

• 得られたデータセットが正規分布に従うと仮定して、データからμとσの値を推定することもできます。
  • データのフィッティングには関数 normfit を使います。
  • 上で作ったμ = 0, σ = 1 の乱数正規分布のデータを使ってパラメータの推定を行います（参考：Statistics Toolbox/正規分布による近似）。

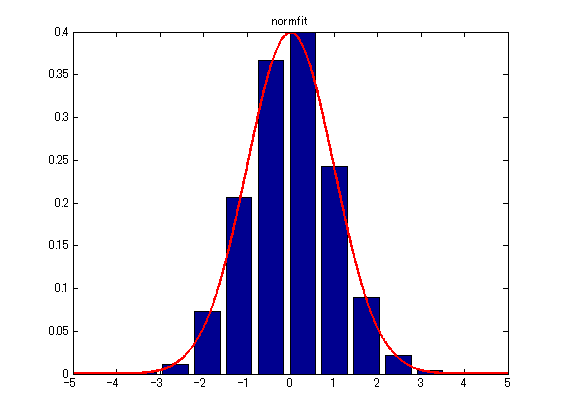
    [muhat,sigmahat,muci,sigmaci] = normfit(data)   % パラメータ推定
    pdfdata = normpdf(linescale, mu, sigma);        % 推定したパラメータから確率密度関数生成
    [histdata, position] = hist(data);              % 乱数正規分布のヒストグラム
    histdata = histdata / (max(histdata) / max(pdfdata)); % ヒストグラムのスケール調整
    figure, bar(position, histdata); xlim([-5,5]);  % プロット
    hold on
    plot(linescale, pdfdata,'r','LineWidth',2); xlim([-5,5]); title('normfit');
    hold off

    
    • ここでは暫定的に、ヒストグラムの頂点と確率密度関数の頂点が一致するようにスケール調整をしていますが、本当ならヒストグラムの面積が１になるように調整するべきです。Statistics Toolbox/正規分布による近似を参考にして下さい。
    • 以下が出力されます。muhatが推定した平均（μ）、sigmahatが推定した標準偏差（σ）です。muci、sigmaciは、それぞれ95%信頼区間です。これらは最尤推定の関数 mle によって計算されます。*3

      muhat =
          0.0017
      sigmahat =
          0.9915
      muci =
         -0.0178
          0.0211
      sigmaci =
          0.9779
          1.0054

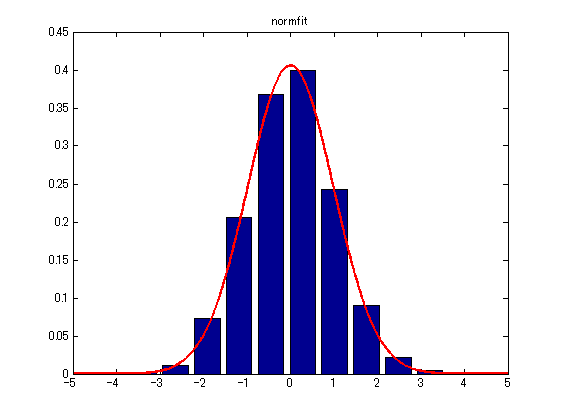
• なお、データが正規分布であることを仮定できるなら、ガウス混合分布モデルの混合数１でも同様のフィッティングができます。

  options = statset('Display','final');
  obj = gmdistribution.fit(data,1,'Options',options);  % 混合数１のGMM
  pdfdata = normpdf(linescale, obj.mu, obj.Sigma);     % GMMパラメータから確率密度関数生成
  figure, bar(position, histdata); xlim([-5,5]);       % プロット
  hold on
  plot(linescale, pdfdata,'r','LineWidth',2); xlim([-5,5]); title('normfit');
  hold off

  

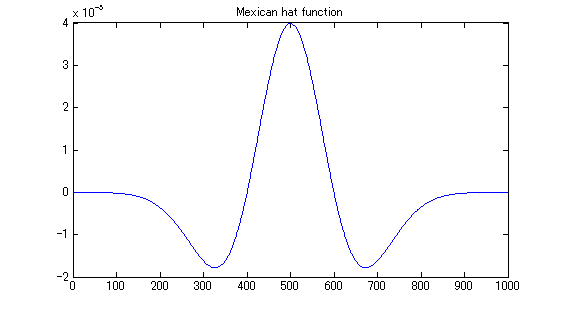
• ちなみに、正規分布の確率密度関数の二次導関数をメキシカン・ハット関数といい*4、ウェーブレット変換 や自己組織化マップ の近傍強化関数*5などに使われています。

  plot( -1 * diff(diff(pdfdata)) ); title('Mexican hat function');

  

• ガウス混合分布モデル
  • 複数の正規分布の混合とみなせるデータセットから、元の各正規分布のパラメータを推定する。

ガンマ分布（Gamma distribution） †

• ガンマ分布 - Wikipedia
  • 形状母数 k、尺度母数 θ から求まる
  • 左に歪んだL字分布。
  • 【引用】 電子部品の寿命分布や通信工学におけるトラフィックの待ち時間分布に応用される。*6*7
  • 蝸牛基底膜の聴覚細胞の応答関数に用いられる（ガンマチャープフィルタ、和歌山大入野先生）

• k = 3, θ = 2.0 のガンマ分布を作ってみます。
  • まずは以下を実行します。

    %パラメータの宣言
    k = 3;
    theta = 2;

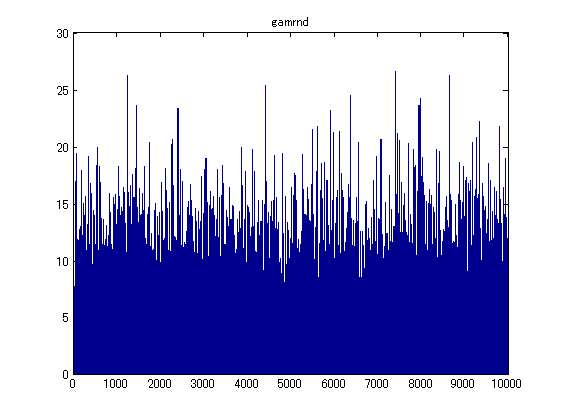
  • この分布に従う乱数を10000個(10000×1の配列で)作るには、関数 gamrnd を使います。

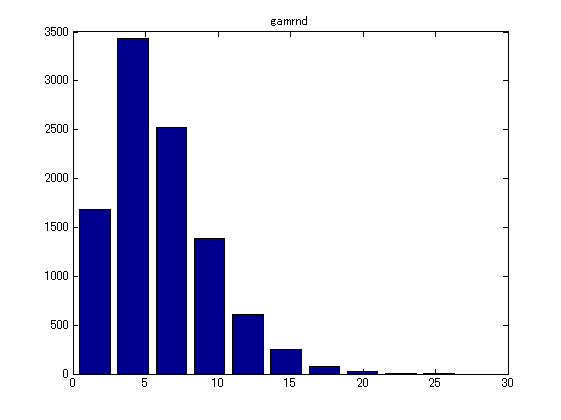
    data = gamrnd(k, theta, [10000 1]);                         % 乱数生成
    bar(data); xlim([0,10000]); title('gamrnd');                % プロット

    
  • ヒストグラムで書いてみます。

    [histdata, position] = hist(data);                          % ヒストグラム
    bar(position, histdata); xlim([0,30]); title('gamrnd');     % プロット

    
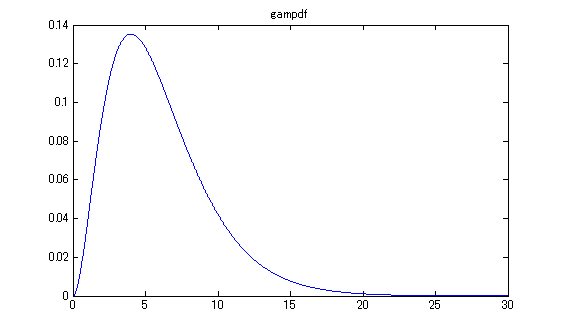
  • より厳密なガンマ分布の確率密度曲線は、関数 gampdf でプロットできます。

    linescale = [0:0.01:30];                                    % x座標のスケール
    pdfdata = gampdf(linescale, k, theta);                      % 確率密度関数生成
    plot(linescale, pdfdata); xlim([0,30]); title('gampdf');    % プロット

    
  • 累積密度曲線は、関数 gamcdf でプロットできます（図は省略）。

    histsum = cumsum(histdata);                                 % ヒストグラムの累積和
    cdfdata = gamcdf(linescale, k, theta);                      % 累積密度関数生成
    subplot(2,1,1); bar(position, histsum); xlim([0,30]); title('gamcdf');
    subplot(2,1,2); plot(linescale, cdfdata); xlim([0,30]);     % プロット

ワイブル分布（Weibull distribution） †

• ワイブル分布 - Wikipedia
  • ワイブル係数（形状パラメータ） m、尺度パラメータ η から求まる
  • 【引用】 m=1は指数分布、m=2はレイリー分布になる*8
  • 左に歪んだL字分布。
  • 【引用】 物体の強度、時間に対する劣化現象や寿命を統計的に記述するために広く利用される*9*10

ロジスティック分布（Logistic distribution） †

• ロジスティック分布 - Wikipedia
  • 第一変数μ 、 第二変数 s から求まる
  • 左右対称の分布。
  • 【引用】 正規分布と同様に対称なS字（シグモイド）型の分布関数、釣鐘型の確率密度関数を持ち一見して両者は類似しているが、ロジスティック分布の方が裾が長く密度関数は平均から離れても下がりにくい*11
  • 【引用】 ロジスティック分布の累積分布関数に見る曲線はロジスティック曲線と呼ばれ、分布そのものよりこちらの曲線の方が様々な場面で現れています*12
    • データが直線で回帰できないときは、ロジスティック関数（曲線）で回帰モデルを作る（ロジスティック回帰）
    • ロジスティック関数の逆関数を ロジット関数 といい、こちらも良く用いられる。
    • ロジスティック関数のさまざまな応用例は ロジスティック分布(Logistic distribution) を参照

ベータ分布（Beta distribution） †

• Beta distribution - Wikipedia
  • 第一変数 p、第二変数 q から求まる （英語版Wikipedia ではαとβ、以下は pとqで統一します）
  • パラメータ次第で左右対称、左に歪んだL字分布、右に歪んだJ字分布を表現できる。
  • 【引用】 独立に一様分布 U(0,1) に従う p+q-1 個の確率変数を大きさの順に並べ替えたとき，小さい方から p 番め（大きい方からは q 番目）の確率変数 X の分布がベータ分布 B(p,q) となる*13
  • 【引用】 工学的な実用例はあまりない*14とされますが、様々な形状の分布を表現できるため統計モデル（一般化線形モデル）の確率分布として注目されています。*15

• p = 2.5, q = 1.5 のベータ分布を作ってみます。
  • まずは以下を実行します。

    %パラメータの宣言
    p = 2.5;
    q = 1.5;

  • この分布に従う乱数を10000個(10000×1の配列で)作るには、関数 betarnd を使います（図は省略）。

    data = betarnd(p, q, [10000 1]);                            % 乱数生成
    bar(data); xlim([0,10000]); title('betarnd');               % プロット

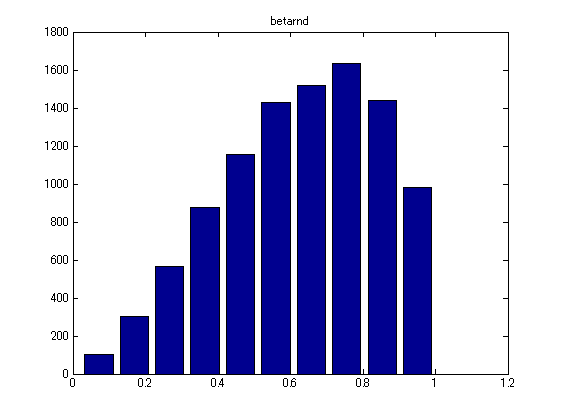
  • ヒストグラムで書いてみます。

    [histdata, position] = hist(data);                          % ヒストグラム
    bar(position, histdata); xlim([0,1.2]); title('betarnd');   % プロット

    
    • x座標の値の範囲は0～1
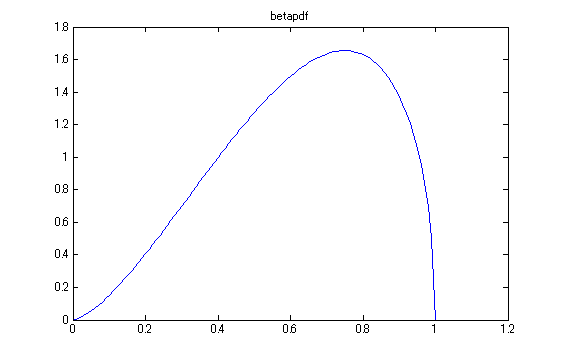
  • より厳密なベータ分布の確率密度曲線は、関数 betapdf でプロットできます。

    linescale = [0:0.01:1.2];                                   % x座標のスケール
    pdfdata = betapdf(linescale, p, q);                         % 確率密度関数生成
    plot(linescale, pdfdata); xlim([0,1.2]); title('betapdf');  % プロット

    

• ベータ分布の確率密度曲線の平均と分散は、関数 betastat で求めることができます。

  [M, V] = betastat(p, q)

• p = 2.5, q = 1.5 のときの平均は0.6250、分散は0.0469です。これは、以下の式でも求めることができます（参考：ベータ分布の性質（関西学院高丹羽先生））。

  M = p / (p + q)
  V = (p * q) / ((p + q) ^ 2 * (p + q + 1))

• 累積密度曲線は、関数 betacdf でプロットできます（図は省略）。

  histsum = cumsum(histdata);                                 % ヒストグラムの累積和
  cdfdata = betacdf(linescale, p, q);                         % 累積密度関数生成
  subplot(2,1,1); bar(position, histsum); xlim([0,1.2]); title('gamcdf');
  subplot(2,1,2); plot(linescale, cdfdata); xlim([0,1.2]);    % プロット

• 得られたデータセットがベータ分布に従うと仮定して、データからpとqの値を推定することもできます。
  • データのフィッティングには関数 betafit を使います。
  • 上で作ったp = 2.5, q = 1.5 の乱数ベータ分布をテストデータとして与えて、このパラメータを推定できるかどうか試してみます。

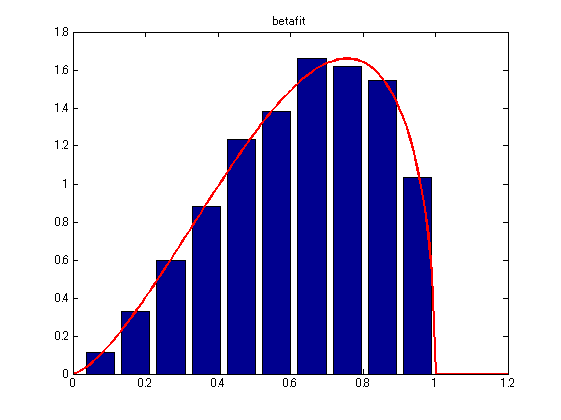
    [phat, pci] = betafit(data)                     % パラメータ推定
    pdfdata = betapdf(linescale, phat(1), phat(2)); % 確率密度関数生成
    [histdata, position] = hist(data);              % 乱数ベータ分布のヒストグラム
    histdata = histdata / (max(histdata) / max(pdfdata)); % ヒストグラムのスケール調整
    figure, bar(position, histdata); xlim([0,1.2]);  % プロット
    hold on
    plot(linescale, pdfdata, 'r','LineWidth',2); xlim([0,1.2]); title('betafit');
    hold off

    
    • ここでは暫定的に、ヒストグラムの頂点と確率密度関数の頂点が一致するようにスケール調整をしていますが、本当ならヒストグラムの面積が１になるように調整するべきです。Statistics Toolbox/正規分布による近似を参考にして下さい。
    • 以下が出力されます。phat(1)が推定したpパラメータ、phat(2)が推定したqパラメータです。pci(:,1)、pci(:,2)は、それぞれpとqの95%信頼区間です。これらは最尤推定の関数 mle によって計算されます。

      phat =
          2.5035    1.4856
      pci =
          2.4353    1.4479
          2.5717    1.5233

    • p = 2.5035、q = 1.4856 になりました。おおむね正しく推定できています。

• ベータ混合分布モデル*16
  • 複数のベータ分布の混合とみなせるデータセットから、元の各ベータ分布のパラメータを推定する。
    • ガウス混合分布モデルでも、ある程度の分布の歪みには頑健に対応できるとのこと。

ディリクレ分布（Dirichlet distribution） †

• ディリクレ分布 - Wikipedia
  • 【引用】ベータ分布を多変量に拡張して一般化した形をしており、そのため多変量ベータ分布とも呼ばれる*17
  • ディリクレ分布とベータ分布の関係に関する議論
    • ベータ分布とディリクレ分布（ryamadaの遺伝学・遺伝統計学メモ）
    • 「統計学関連なんでもあり」BBS
• Infinite Mixture Model（ディリクレ分布（など）に基づく混合分布モデル）

離散変数（Categorical variable） †

• 離散的に変化する値（二値のみ、整数のみ等）の出現頻度を扱う分布。
  • 【引用】 サイコロを投げるような場合における確率関数（略）。確率変数は離散的な値だけを取ることができます。このような場合を離散型分布といいます*18

二項分布（Binomial distribution） †

• 二項分布 - Wikipedia
  • 成功確率 p 、試行回数 n から求まる
  • 左右対称の分布
  • 【引用】 結果が成功か失敗のいずれかである n 回の独立な試行を行ったときの成功数で表される離散確率分布である（各試行における成功確率 p は一定である）*19
  • 【引用】 ある集団において，特性 A を持つものの割合が p であり，持たないものの割合が q であるとする（ p+q=1 ）。このとき，集団から無作為に n 人を抽出したとき，特性 A を持つものが x 人である確率を考える*20

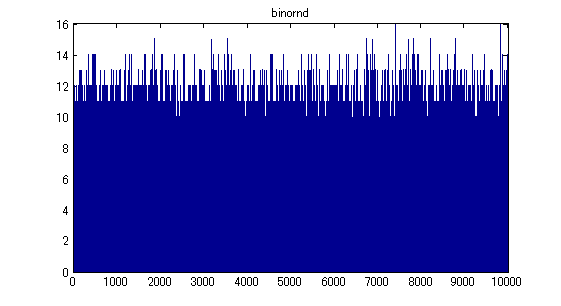
• n = 20, p = 0.4 の二項分布を作ってみます。
  • まずは以下を実行します。

    %パラメータの宣言
    n = 20;
    p = 0.4;

  • この分布に従う乱数を10000個(10000×1の配列で)作るには、関数 binornd を使います。

    data = binornd(n, p, [10000 1]);                            % 乱数生成
    bar(data); xlim([0,10000]); title('binornd');               % プロット

    
    • ここで出力される値が意味するのは「『成功率0.4の試行を20回行ったとき、（20回中）何回成功するか』の実験を10000回実施した」ということです。

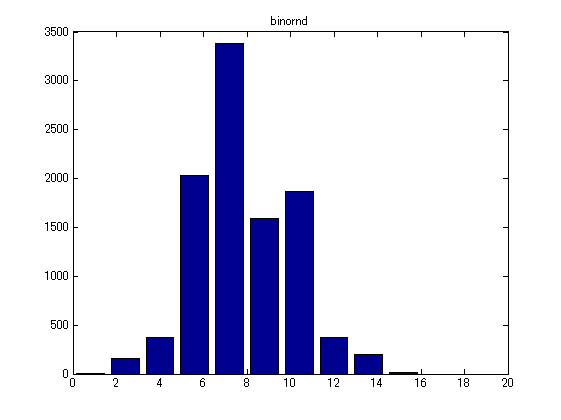
• ヒストグラムで書いてみます。

  [histdata, position] = hist(data);                          % ヒストグラム
  bar(position, histdata); xlim([0,20]); title('binornd');    % プロット

  

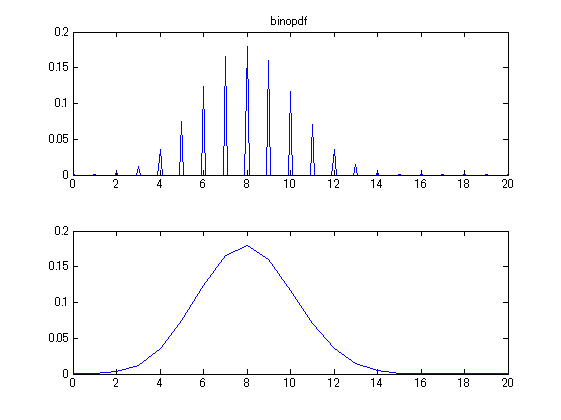
• ヒストグラムの頂点を結んだ線が確率密度曲線（の近似）になります。より厳密な二項分布の確率密度曲線は、関数 binopdf でプロットできます。ここでは x座標 0 ～ 20 までの区間について「0.1刻み」と「1刻み」の二通りで関数生成＆プロットしてみます。

  linescale1 = [0:0.1:20];                          % x座標のスケール（0.1刻み）
  pdfdata1 = binopdf(linescale1, n, p);             % 確率密度関数生成
  linescale2 = [0:1:20];                            % x座標のスケール（1刻み）
  pdfdata2 = binopdf(linescale2, n, p);             % 確率密度関数生成
  subplot(2,1,1); plot(linescale1, pdfdata1); xlim([0,20]); title('binopdf');
  subplot(2,1,2); plot(linescale2, pdfdata2); xlim([0,20]);   % プロット

  
  • このように、離散分布の関数は、x座標に連続値（小数点を含む値）を指定しても、x座標の値が整数のとき以外は0を出力します。
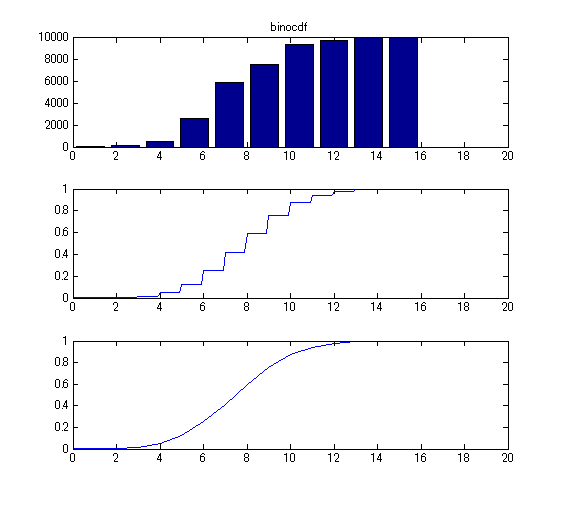
• ヒストグラムの各バーを、x座標の小さいものから順に足しあわせてプロットしていけば累積密度曲線（の近似）になります。より厳密な二項分布の累積密度曲線は、関数 binocdf でプロットできます。

  histsum = cumsum(histdata);                       % ヒストグラムの累積和
  cdfdata1 = binocdf(linescale1, n, p);             % 累積密度関数生成（0.1刻み）
  cdfdata2 = binocdf(linescale2, n, p);             % 累積密度関数生成（1刻み）
  subplot(3,1,1); bar(position, histsum); xlim([0,20]); title('binocdf');
  subplot(3,1,2); plot(linescale1, cdfdata1); xlim([0,20]);
  subplot(3,1,3); plot(linescale2, cdfdata2); xlim([0,20]);   % プロット

  

ポアソン分布 †

• 【引用】 1 回ごとの事象の生起確率 p が一定であるとき，実験を繰り返し行うことを ベルヌーイ試行 というが，独立に実験を n 回繰り返したとき，x 回事象が生じる確率は二項分布である。ポアソン分布は、二項分布の中でも特に出現確率の低い事象を扱うとき、よくあてはまる。*21
• 【引用】 製品中の不良品の個数，一定時間内に電話がかかってくる回数などがあげられる。*22
  • 値に上限と下限をもつような、「閉じた尺度」のデータはポアソン分布に近づく。
    • 0%～100%、0点～100点など。こういったデータは分布の中心が端に近づくにつれて分布の裾野がつまり（天井効果、フロア効果）、L字型やJ字型のポアソン分布を作りやすい。
    • 片方にのみ開いた尺度（負値を持たないデータ、年収など）も、裾野が引っ張られてポアソン分布を作る。

ベルヌーイ分布 †

分布形状の測定 †

• 以下、Statistics Toolbox / 形状の測度 に基づきます。

尖度 kurtosis と 歪度 skewness †

• 尖度：分布の頂点がどれだけ尖っているか。
  • 【引用】 正規分布と比べて、尖度が大きければ鋭いピークと長く太い裾を持った分布を持ち，尖度が小さければより丸みがかったピークと短く細い尾を持った分布であるという事が判断できる。(略)正規分布の尖度を0とする定義と3とする定義があることに注意*23
  • MATLABの kurtosis 関数では、正規分布は尖度3になり、尖っているほど値が大きくなる
• 歪度：分布の左右がどれだけ非対称か。
  • 【引用】 確率分布の分布特性を示すためには期待値および分散が通常用いられるが、分布型の違いを示す指標の１つに3次モーメント（3乗の期待値）と4次モーメント（4乗の期待値）がある。（略）平均と分散の影響を除くように標準化された3次モーメントと標準化された4次モーメントを考える。（略）標準正規確率変数の分布に歪みはなく、0を中心に左右対称であるから歪度は0である。歪度の符号により正の歪み、負の歪みを持つ分布といわれる。（略）Z の4次モーメント E (Z4) - 3 は尖度 β2 と呼ばれる*24
  • 正規分布（左右対称の分布）では歪度０、L字型分布は歪度＋、J字型分布は歪度－

• 上で作った 正規分布 と ガンマ分布 の尖度、歪度を比べてみます。

  mu = 0; sigma = 1;
  dataNorm = normrnd(mu, sigma, [10000 1]);    % 正規分布に従う10000個の乱数
  k = 3; theta = 2;
  dataGam  = gamrnd(k, theta, [10000 1]);      % ガンマ分布に従う10000個の乱数
  
  k = kurtosis([dataNorm dataGam])       % 尖度（1列目：正規分布、2列目：ガンマ分布）
  y = skewness([dataNorm dataGam])       % 歪度（1列目：正規分布、2列目：ガンマ分布）

  • 引数のベクトルは確率密度曲線ではなく、それぞれの分布に従う乱数（ヒストグラムを書く前の生データ）であることに注意して下さい。
  • 結果

        (正規)   (ガンマ)
    k =
        2.9537    5.4342
    
    y =
       -0.0096    1.1623

• 正規分布の尖度は3、歪度は0に近くなっています。
• ガンマ分布の尖度は正規分布より大きく、歪度は正の値になっている（L字に近い）ことがわかります（これは k=3, θ=2.0 のガンマ分布の場合なので、他のパラメータを指定すれば尖度、歪度は変わります）。

• なお、歪度の大きい分布の形状を正規分布に近づけるための変換手法が提案されています。量的分析法 勉強会/確率分布/標本分布が正規分布ではないが、ANOVAを使いたい場合 を参照して下さい。

中心モーメント moment †

百分位数値（パーセンタイル）prctile と 分位数（クォンタイル） quantile †

標準化z得点 zscore †

分布形状の検定 †

• あるデータ群が正規分布に従っているかどうかを検定したいときは、1標本コルモゴルフ-スミルノフ検定 を使います。
• ２つのデータ群の分布が一致しているかどうかを検定したいときは、2標本コルモゴルフ-スミルノフ検定 を使います。
• その他
  • Matlabによる初歩の検定（理研 最上先生） でも、kstwo.m を公開なさっています。
  • Rによるコルモゴロフ・スミルノフ検定の実例
  • QQプロット（正規性検定）

検索

更新履歴

最新の20件

edit
限定版