R Note/音響解析データの統計解析

Last-modified: 2016-10-21 (金) 12:42:29

Top / R Note / 音響解析データの統計解析

音響解析（音声コーパス）データの統計解析 †

音響解析（音声コーパス）データの統計解析

↑

→ これは話者数の少ないデータなので、下記の図表と結果が一致しないことにご注意ください。

CSJの音声データファイルの冒頭120秒をMFCC解析した結果。各列の意味は下記の通り。

filename	CSJのファイル名。12ファイルある。
register	レジスタ名。"APS"は学会講演録音。"Re-Read"は学会講演録音の再朗読。
speakerID	話者名。APSとRe-Readについて同じ話者がいるため、6話者。
gender		話者の性別。
seg		音素名。SclSは<cl>、SsvSは<sv>。音素ラベルのないフレームは書き出していない。
segID		音素ID。各ファイルについて音素ごとに数値をつけている。
frameID		フレームID。各ファイルについて0.01秒ごとに数値をつけている。
beg_time	フレームの開始時間。
MFCC1～MFCC12	MFCC12次元の解析結果。
C0		パワーの解析結果。
dMFCC1～dMFCC12	デルタMFCC12次元の解析結果。
dC0		デルタパワーの解析結果。

ここでの「フレーム」は音声解析の分析窓のことで、以降の「データテーブル（データフレーム）」とは別です。
解析の詳細は MFCC解析のツール/HTK(Hidden Markov Model Toolkit) 付属の HCopy を使うを参照

↑

パッケージインストール †

Rを起動して以下のコマンドを実行します。初回に一回だけ実行すれば、以降は不要です。
install.packages("plyr") #データテーブルの集計用パッケージ

install.packages("ggplot2") #視覚化のためのパッケージ

install.packages("reshape") #データテーブルの整形用パッケージ

install.packages("lme4") #一般化線形モデルのためのパッケージ

install.packages("lmerTest") #一般化線形モデルの検定のためのパッケージ

install.packages("pwr") #検定力解析（パワーアナリシス）のためのパッケージ

↑

データテーブルの読み込み †

ダウンロードした CSJ_MFCC26_short.zip を解凍し、右クリックして、ファイルの場所（パス）を取得します。例えば E:\Users\m-kouki\Desktop にあるとします。
Rを起動して、以下を実行*1
data <- read.table("E:/Users/m-kouki/Desktop/CSJ_MFCC26.txt", header = T)

パスの区切り文字は「/」または「\\」
今回のデータの1行目はヘッダ（各列のデータの詳細を説明したラベル）があるので、header = Tを指定しました。ヘッダが無いときは F を指定します。ヘッダは極力つけるようにしてください。
参考：R-Source 40. ファイルからデータを読み込む（中央農業総合研究センター竹澤先生）

読み込まれたデータは変数 data に格納されます。以下のような操作が可能です。
data #データテーブルの中身を見る

head(data) #データテーブルの冒頭数行を見る

names(data) #変数名の一覧を得る

 [1] "filename"  "register"  "speakerID" "gender"    "seg"       "segID"     "frameID"  
 [8] "beg_time"  "MFCC1"     "MFCC2"     "MFCC3"     "MFCC4"     "MFCC5"     "MFCC6"    
[15] "MFCC7"     "MFCC8"     "MFCC9"     "MFCC10"    "MFCC11"    "MFCC12"    "C0"       
[22] "dMFCC1"    "dMFCC2"    "dMFCC3"    "dMFCC4"    "dMFCC5"    "dMFCC6"    "dMFCC7"   
[29] "dMFCC8"    "dMFCC9"    "dMFCC10"   "dMFCC11"   "dMFCC12"   "dC0"

データの一部分を指定することができます。
data[ , 1:4] #1列目から4列目までの全ての行

data[ 1:4 ,] #1行目から4行目までの全ての列

↑

データの前処理 †

↑

要約統計量を得る †

以下を実行します。
summary(data)

データの尺度によって出力される結果が違うことに注意してください。
- 連続型変数 Area, Slope, Soil.pH, Worm.density は6つの統計量が出力される。平均値のみパラメトリックな量、他の5つはノンパラメトリックな量。カテゴリカル型変数は水準ごとに数え上げられる。*2

カテゴリカル変数のつもりで作成したデータが、summaryを表示した結果連続型変数として扱われる場合があります。この例では、例えばspeakerIDは以下のようにsummaryが出力されます。
```
  speakerID  
Min.   :1.000
1st Qu.:2.000
Median :4.000
Mean   :3.596
3rd Qu.:5.000
Max.   :6.000
```
実際には、speakerIDの数値はID番号なので、平均値や中央値に意味はありません。以後の統計計算で不備が出る場合があるので*3、このようなデータはカテゴリカル変数であることを明示しておきます。*4
data$speakerID <- factor(data$speakerID)

data$segID <- factor(data$segID)

data$frameID <- factor(data$frameID)

もう一度summaryを確認します。
summary(data)

データの総数は以下で求められます。
nrow(data)

↑

特定のデータを抜き出す †

単に特定の列だけ抜き出したい場合、例えば以下のように書けます。
data[ c("speakerID","MFCC1") ]

条件に該当する行だけ抜き出したい場合、例えば以下のような方法がある。
data[ C0 > 20 & gender == "F" , 1:9] # C0の値が20以上の女性の行、列は1から9まで出力

subset関数を使うやり方が便利。Rデータフレームから一部を抜き出す（upaksta’s blog）が詳しい。
subset(data, (C0 > 20) & (gender == "F"), select = 1:9 )

ヘッダ名を指定して取り出すこともできる。
subset(data, (C0 > 20) & (gender == "F"), select = c(speakerID, MFCC1) )

特定のデータのみを抜き出して新しいデータテーブルを作ることもできる。
dataF <- subset(data, (gender == "F")) # 女性のみを取り出してdataFを作る

summary(dataF)

欠損値を除外したい場合は na.omit 関数を使う。
data <- na.omit(data)

どれか一つの列に欠損値を含んでいた場合、その行ごと削除される。

複数の条件で抜き出したデータテーブルを結合する場合は、rbind関数を使う。
dataV <- rbind( subset(data, seg=="i"), subset(data, seg=="e"), subset(data, seg=="o"), subset(data, seg=="a"), subset(data, seg=="u") ) #短母音5つのみを取り出してdataVを作る

summary(dataV)

特定のデータを抜き出した後のデータテーブルをsummaryすると、カテゴリカルデータのカウント数が"0"になって出力される場合がある。
```
      seg    
a      :3519
o      :3451
u      :3304
i      :1719
e      :1514
aH     :   0
(Other):   0
```
再度factor関数にかけてやると、カウント数0のデータは消える。
dataV$seg <- factor(dataV$seg)

summary(dataV)

↑

特定のデータの計算結果を追記する †

MFCC1～MFCC12の平均を求めて、データテーブルに"MFCC.Mean"という列名で追記してみます。
data$MFCC.Mean <- (data$MFCC1 + data$MFCC2 + data$MFCC3 + data$MFCC4 + data$MFCC5 + data$MFCC6 + data$MFCC7 + data$MFCC8 + data$MFCC9 + data$MFCC10 + data$MFCC11 + data$MFCC12) / 12

apply関数を使うこともできます。
data$MFCC.Mean <- apply(data[, 9:20], 1, mean)

各行について集計したい場合は第二引数に1、各列について集計したい場合は第二引数に2を指定します。

値のどこかにNaNを含む可能性があって、その値を除外して平均を求めたい場合
data$MFCC.Mean <- apply(data[, 9:20], 1, mean, na.rm=TRUE)

dMFCC1～dMFCC12の二乗和*5を求めて、データテーブルに"dMFCC.SquareSum"という列名で追記してみます。
data$dMFCC.SquareSum <- data$dMFCC1^2 + data$dMFCC2^2 + data$dMFCC3^2 + data$dMFCC4^2 + data$dMFCC5^2 + data$dMFCC6^2 + data$dMFCC7^2 + data$dMFCC8^2 + data$dMFCC9^2 + data$dMFCC10^2 + data$dMFCC11^2 + data$dMFCC12^2

summary(data)

対数変換したデータを追記する
data$dMFCC.SquareSum.log = log(data$dMFCC.SquareSum)

C0を平均値が0、分散が1になるように標準化したC0.scale列を追記する*6 *7
data$C0.scale = scale(data$C0)

summary(data)

列名は C0.scale.V1 になっている。→ 理由は？

【発展】条件を指定してデータを追記するには、transform 関数を使う。例えば、「短母音5種類には"sV"、それ以外には"etc"というラベルをつけ、新たに"seg2"という列名で追記したいとする。以下のように書ける。
data = transform(data, seg2 = ifelse( ( (seg == "i") | (seg == "e") | (seg == "o") | (seg == "a") | (seg == "u") ) , "sV", "etc" ) )

さらに条件を複雑にして、「短母音5種類には"sV"、長母音5種類には"lV"、それ以外には"etc"というラベルをつけ、新たに"seg3"という列名で追記したい場合は、以下。
data = transform(data, seg3 = ifelse( ( (seg == "i") | (seg == "e") | (seg == "o") | (seg == "a") | (seg == "u") ) , "sV", ifelse( ( (seg == "iH") | (seg == "eH") | (seg == "oH") | (seg == "aH") | (seg == "uH") ) , "lV", "etc" ) ) )

【発展】特定のデータを含む行に隣接する行のデータを得る
- 例えば、「短母音の行の直前と直後の行を探して、該当する行には"1"、それ以外には"0"というラベルをつけ、新たに"seg.neighbor"という列名で追記したいとします。
- データテーブルの基本的な考え方は、「1行の中に解析に必要なデータが全て含まれていること」です。したがって、今回の処理を扱う前に、「各行の直前と直後の行を、新しい列として追加する」処理を行います。（※注この処理は、あえてRを使って行うよりも、Excelなどの表計算ソフトで行うほうが簡単です。）
  - まずは、seg列のみを取り出して新しいデータテーブルdata.segを作ります。
    data.seg = data[ c("seg") ]

空欄を意味する1行1列のデータテーブルを作ります。
seg.nothing = data.frame(seg=c("Nothing"))

data.segを前に1列ずらしたデータテーブル data.seg.prev と、後に1列ずらしたデータテーブル data.seg.next を作ります。data.segの冒頭、または最後に空欄のデータテーブルを結合します。
data.seg.prev = rbind(seg.nothing, data.seg)

data.seg.next = rbind(data.seg, seg.nothing)

続いて、data.seg.prev の最初の列、 data.seg.next の最後の列を除外します。
data.seg.prev = data.seg.prev[1:(nrow(data.seg.prev)-1) , ]

data.seg.next = data.seg.next[2:nrow(data.seg.next) , ]

元のデータテーブル data に data.seg.prev と data.seg.next を結合します。
data$seg.prev = data.seg.prev

data$seg.next = data.seg.next

head(data)

これで、必要な情報は全て1行の中に集約されました。

transform関数を使って該当条件のラベルを付加します。
data = transform(data, seg.neighbor = ifelse( ( (seg.prev == "i") | (seg.prev == "e") | (seg.prev == "o") | (seg.prev == "a") | (seg.prev == "u") | (seg.next == "i") | (seg.next == "e") | (seg.next == "o") | (seg.next == "a") | (seg.next == "u") ) , "1", "0" ) )

このサンプルデータは各行が「フレーム（分析窓）」単位で書かれているため、この処理を実行しても「短母音のフレームの直前と直後の１フレーム」が該当するだけです。音素単位で処理をしたい場合は、音素単位のデータテーブルを作ってください。

↑

特定のデータの集計値を得る †

ddply関数が大変便利です*8。パッケージplyrとは（浅井拓也氏）が詳しいです。
plyrパッケージのインストールが完了していれば、ライブラリを呼び出すだけでOKです。
library(plyr)

様々な実例は「plyrパッケージで君も前処理スタ☆」改め「plyrパッケージ徹底入門」（tera monagi氏）が詳しいです。

各話者・各レジスタごとに、C0の平均値と標準偏差を求めて、新しいデータテーブル dataSumm に C0mean, C0sd という列名で追記するには、以下のようにします。
dataSumm <- ddply(data, c('speakerID', 'register'), summarize, C0mean = mean(C0), C0sd = sd(C0) )

dataSumm

指定した条件ごとの集計値が出力されます。

   speakerID register   C0mean     C0sd
1          1      APS 15.69648 2.949087
2          1  Re-Read 13.24777 2.565976
3          2      APS 15.75885 2.861640
4          2  Re-Read 13.95841 2.957040
5          3      APS 14.53344 2.584729
6          3  Re-Read 14.81330 2.511646
7          4      APS 13.91550 2.801826
8          4  Re-Read 13.18621 3.143895
9          5      APS 15.02620 2.385534
10         5  Re-Read 14.91980 3.005093
11         6      APS 15.10699 2.306960
12         6  Re-Read 14.23184 2.976182

各話者・各レジスタごとに、C0の平均値と標準偏差を求めて、もとのデータテーブル data に C0mean, C0sd という列名で追記するには、以下のようにします。
data <- ddply(data, c('speakerID', 'register'), transform, C0mean = mean(C0), C0sd = sd(C0) )

data

元のデータに列が追加されています。

各話者について、C0の値の平均値が0、標準偏差が1になるようにZスコア変換*9したC0.z列を追記する*10
data <- ddply(data, c('speakerID'), transform, C0.z = (C0 - mean(C0) ) / sd(C0) )

head(data)

【発展】特定条件の集計値を全行に追加する
- 例えば「レジスタAPSに限定して、話者ごとにC0の平均値を求め、（レジスタRe-Readを含む）すべての行にC0_APSmeanという列名で追記する」には以下のようにします。
  #レジスタAPS以外のC0値をNAにした新しい列「C0_APS」を作り、dataに追記する
  
  data = transform(data, C0_APS = ifelse( register == "APS", C0, NA ) )
  
  #各話者のAPSのC0の平均値を求めて、すべての行に追記する
  
  data = ddply(data, c('speakerID'), transform, C0_APSmean = mean(na.omit(C0_APS)) )

【発展】フレーム単位のデータテーブルから音素単位のデータテーブルに変換する
- サンプルデータ data の各行は、窓長0.01秒の時間フレームです。これを、コーパス解析で一般的な「各行が一つの音素」のデータテーブルに変換してみます。
- segIDについて集計値を求めます。segIDは異なる話者で重複する場合があるので、'speakerID' と 'segID' で集計すれば、全ての音素を１回ずつ拾うことができます。ここでは各音素の MFCC1 の平均値を出力しています。
  data2 <- ddply(data, c('speakerID', 'segID'), summarize, MFCC1 = mean(MFCC1) )
  
  nrow(data2)

```
[1] 7153
```

他のfactor変数を条件に加えても構いません。データの総行数は変化しません。
data2 <- ddply(data, c('filename', 'register', 'speakerID', 'gender', 'seg', 'segID'), summarize, MFCC1 = mean(MFCC1)) )

nrow(data2)

```
[1] 7153
```

よく行われる処理は、各音素について時間フレームの中心（その音素の時間的中心点）の1フレームを取り出し、その音素の代表値とすることです*11
data2 <- ddply(data, c('speakerID', 'segID'), summarize, MFCC1 = MFCC1[round(length(MFCC1)/2)] )

length(MFCC1) は各条件で抽出されたMFCC1のベクトルサイズ、各音素のフレーム長に相当
round(length(MFCC1)/2) は各音素のフレーム長の半分を四捨五入したもの、各音素の時間的中心点のフレーム番号に相当
MFCC1[round(length(MFCC1)/2)] は各音素の時間的中心点のフレームのMFCC1の値

↑

外れ値を除外する †

ddply関数を使って、「話者＆レジスタごとにC0の平均値と標準偏差（SD）を求めて、平均値±2.0SD をこえる値」は外れ値として除外してみます。
まず、平均値＋2.0SD を上回る値は1、そうでない値は0をつけ、"C0out1"という列名で追記します。
data <- ddply(data, c('speakerID', 'register'), transform, C0out1 = ifelse(C0 - (mean(C0) + ( 2.0 * sd(C0) )) > 0, 1, 0 ))

続いて、平均値－2.0SD を下回る値は1、そうでない値は0をつけ、"C0out2"という列名で追記します。
data <- ddply(data, c('speakerID', 'register'), transform, C0out2 = ifelse(C0 - (mean(C0) - ( 2.0 * sd(C0) )) < 0, 1, 0 ))

C0out1またはC0out2が1になっている行ははずれ値として削除して、新しいデータテーブル data2 に保存します。データの重複を防ぐため、rbindは使わず別々に処理します。
data2 = subset(data, C0out1=="0")

data2 = subset(data2, C0out2=="0")

nrow(data)

nrow(data2)

↑

ランダムサンプリング †

ddply関数を使えば、指定した各条件について、該当するデータから指定した個数のデータをランダムに選択する（ランダムサンプリング）こともできます。
話者＆レジスタ＆各音素カテゴリーごとに、C0とdC0をそれぞれ10個ランダムに選択し、新しいデータテーブル dataRand を作るには、以下のようにします。
sampling = 10

dataRand = ddply(data, c('speakerID', 'register', 'seg'), summarize, C0 = sample(C0, sampling, replace = T), dC0 = sample(dC0, sampling, replace = T) )

dataRand

サンプリングしたC0とdC0の行番号は一致していない（それぞれ別々にサンプリングした）ことに注意してください。
"replace = T"は、データが重複してサンプリングされることを許可しています。F を指定すると重複サンプリングを行いませんが、その場合、総データ数が sampling を下回る条件が含まれているとエラー*12になります。

↑

データの視覚化 †

データの特性を理解するために、視覚化はとても重要です。

↑

準備 †

ggplot2関数が大変多機能で、便利です*13。ggplot2 : データの可視化（苦労する遊び人の玩具箱）を参照して下さい。
ggplot2パッケージのインストールが完了していれば、ライブラリを呼び出すだけでOKです。plyrパッケージ、reshapeパッケージのライブラリも呼び出しておきます。
library(ggplot2)

library(plyr)

library(reshape)

サンプルデータ CSJ_MFCC26_short.zip をダウンロードしてください。
以後の説明では、短母音のみのデータテーブルを使います。
data <- read.table("E:/Users/m-kouki/Desktop/CSJ_MFCC26.txt", header = T)

data$speakerID = factor(data$speakerID)

data$segID = factor(data$segID)

data$frameID = factor(data$frameID)

dataV = subset(data, (seg=="i")|(seg=="e")|(seg=="o")|(seg=="a")|(seg=="u") )

summary(dataV)

↑

散布図 †

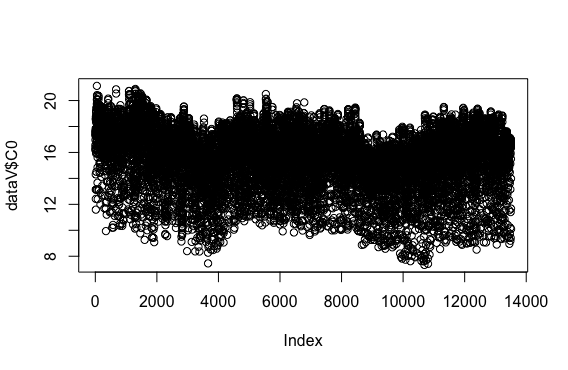
単にplot関数に１つのデータ列を与えると、散布図になります。
plot(dataV$C0)

縦軸がC0の値、横軸は左からデータの行数です。
ここで、分析に使う各パラメータの散布図を確認しておくと良いでしょう。明らかな分析ミスや外れ値の傾向などを把握するのに役立ちます。例えば、話者による差が著しく大きいのであれば、Zスコア変換などを検討します。

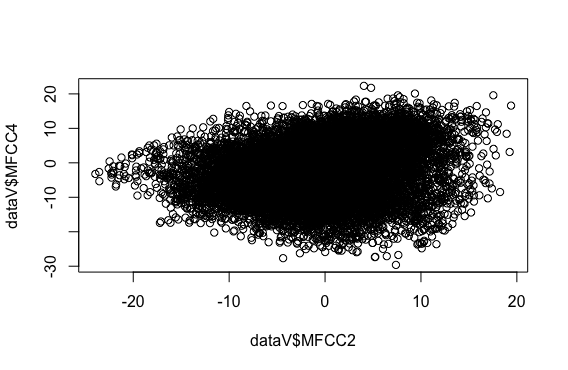
plot関数に２つのデータ列を与えてみます。
plot(dataV$MFCC2, dataV$MFCC4)

ここでは、縦軸がMFCC4の値、横軸がMFCC2の値です。
女性話者のデータに限定してみます。
plot(subset(dataV, gender=="F")$MFCC2, subset(dataV, gender=="F")$MFCC4)

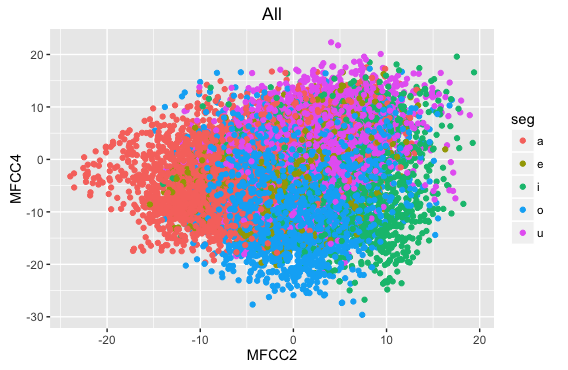
ggplotを使うと、条件ごとの色分けも簡単にできます。以下は母音カテゴリーごとに色分けをした例です。
ggplot(dataV) +

geom_point(aes(x=MFCC2, y=MFCC4, color=seg)) +

labs(title="All")

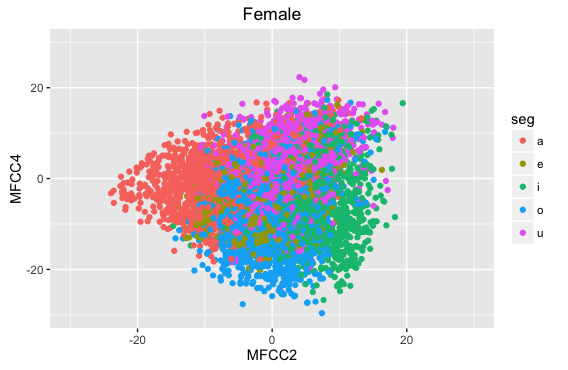
女性話者のデータに限定してみます。後でグラフに機能を追記するために、変数 p に代入して実行してみます。
p = ggplot(subset(dataV, gender=="F")) +

geom_point(aes(x=MFCC2, y=MFCC4, color=seg)) +

labs(title="Female")

p

グラフの軸のサイズを指定することもできます。上記の変数 p に追記して実行します。
p = p + xlim(-30, 30) + ylim(-30, 30)

p

ddplyと組み合わせると色々と便利です。
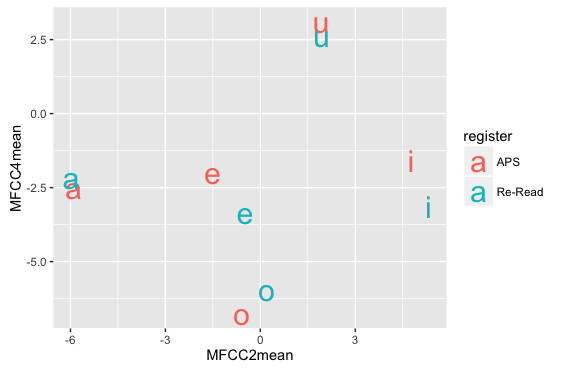
- 母音ごと・レジスタごとに平均値を求めて、レジスタで色分けして母音名をテキストでプロット
  dataSumm = ddply(dataV, c('seg', 'register'), summarize, MFCC2mean = mean(MFCC2), MFCC4mean = mean(MFCC4) )
  
  ggplot(dataSumm) +
  
  geom_text(aes(x=MFCC2mean, y=MFCC4mean, label=seg, colour=register), size=8)

散布図の各点を文字にしたい場合は、geom_textを使います。文字サイズはsizeで指定しています。

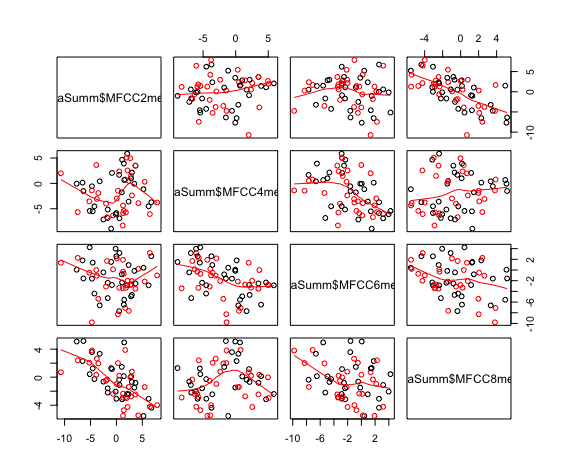
話者ごと・母音ごと・レジスタごとにMFCC2, MFCC4, MFCC6, MFCC8の平均値を求めて、各組み合わせの散布図と平滑化曲線をプロット（参考:RjpWiki グラフィックス参考実例集：散布図行列
dataSumm = ddply(dataV, c('speakerID', 'seg', 'register'), summarize, MFCC2mean = mean(MFCC2), MFCC4mean = mean(MFCC4), MFCC6mean = mean(MFCC6), MFCC8mean = mean(MFCC8) )

pairs(~dataSumm$MFCC2mean + dataSumm$MFCC4mean + dataSumm$MFCC6mean + dataSumm$MFCC8mean, col=dataSumm$register, data=dataSumm, panel=panel.smooth)

これはggplotを使っていません。*14

↑

ヒストグラム †

分析の最初のチェックとして、ヒストグラムの形状は非常に重要です。
- 分析に用いる各要因の各水準ごとにヒストグラムをプロットしてみて、どれかが２峰性の分布になっていた場合、通常の統計の結果は信頼性の低いものになってしまいます。２峰性分布があらわれる原因としては、解析の失敗（一貫した、無視できない量のエラーやはずれ値）や、考慮すべき要因を入れていない（基本周波数における男女差など）、実験計画のミス、なんらかの被験者バイアス、などいろいろ考えられます。
- 単峰性でも、ヒストグラムの形状がゆがんでいる場合、注意深く検討する必要があります。詳しくはR Note/統計/確率分布/正規分布でない標本を正規分布に近づけるを参照して下さい。形状のゆがみを統計的に解析する方法として、一群のヒストグラムの歪度と尖度を求めるなどがあります。
全てのデータのMFCC1のヒストグラムを、通常の方法でプロット
hist(dataV$MFCC1)

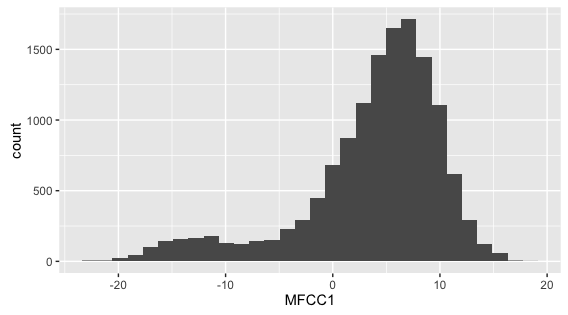
ggplotを使用した方法
ggplot( dataV, aes(x = MFCC1) ) + geom_histogram()

全データのMFCC1は２峰性の分布になっています。各要因・各水準で見て単峰性になっていれば問題はないので、実際に確認する必要があります。

ggplotとsubplotを組み合わせると、各要因・各水準のヒストグラムを並べて表示できるため、便利です。
- 話者別にヒストグラムをプロット
  ggplot(dataV) +
  
  geom_histogram( aes(x = MFCC1) ) +
  
  facet_wrap(~speakerID)

レジスタ・話者・母音別にヒストグラムをプロット
ggplot(dataV) +

geom_histogram( aes(x = MFCC1) ) +

facet_wrap(register~speakerID~seg)

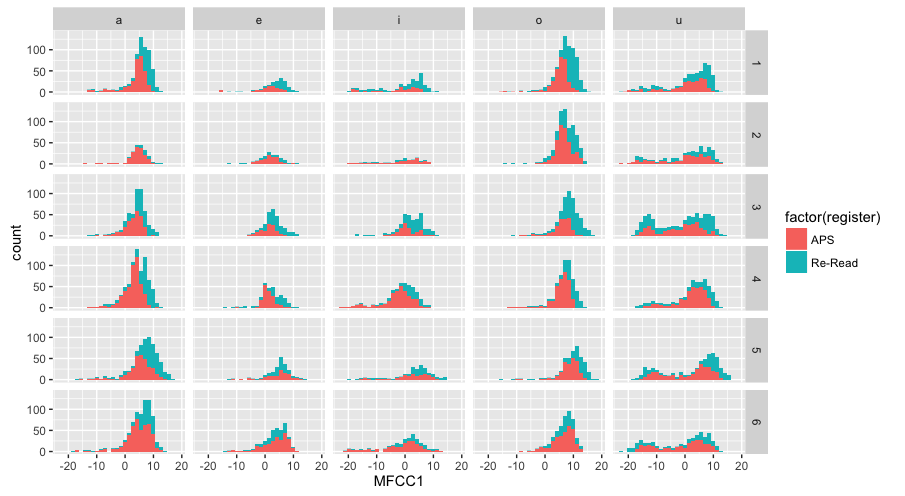
レジスタで色分けして、話者を縦グリッド・母音を横グリッドにしてヒストグラムをプロット*15
ggplot(dataV) +

geom_histogram( aes( x = MFCC1, fill=factor(register) ) ) +

facet_grid(speakerID~seg)

/u/では全ての話者で二峰性の分布になっていることが分かります。おそらく、これは音響解析のエラーであろうと予想できます。

多次元ヒストグラム
- R generate 2D histogram from raw data
- 二変量データのヒストグラムと密度推定 *16

↑

箱ヒゲ図（ボックスプロット）*17 †

t検定や分散分析の前に、データの分布や有意傾向を視覚的に確認するために、箱ヒゲ図が便利です。
全てのデータのMFCC1の箱ヒゲ図を、通常の方法でプロット
boxplot(subset(dataV, select = c(MFCC1)))

複数の列の値を同時にプロットすることもできます。
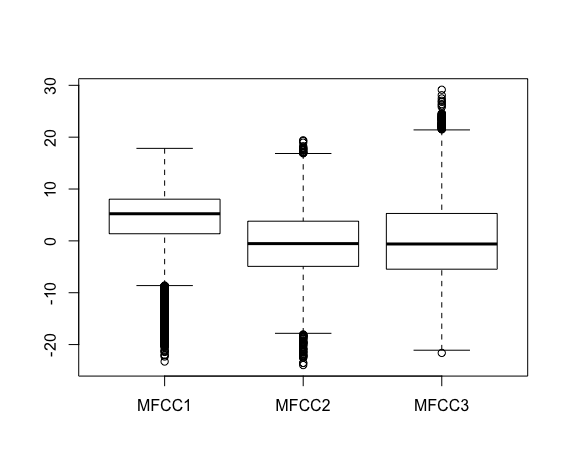
boxplot(subset(dataV, select = c(MFCC1, MFCC2, MFCC3) ) )

箱ヒゲ図の見方は以下の通りです。 *18
- 中央の横線：各データの全体の中央値（第2クォンタイル*19）
- 箱の上端の線：全体の中央値より大きいデータの中央値（第3クォンタイル）
- 箱の下端の線：全体の中央値より小さいデータの中央値（第1クォンタイル）
- 箱の中に、データ全体の約50%が含まれます。上下のヒゲは、デフォルト設定では箱の長さの1.5培です。
- ヒゲの外側にある値は、はずれ値として扱われます。

全てのデータのMFCC1の箱ヒゲ図を、ggplotでは以下のように書いて表示します。
ggplot(dataV) +

geom_boxplot(aes(y = MFCC1, x = "MFCC1"))

ggplotは、boxplotと特性が異なります。boxplotは異なる列のデータを並列して表示するのに向いているのに対してggplotは、カテゴリカル変数型の列内の変数（factor）ごとにデータを並列して表示するのに向いています。

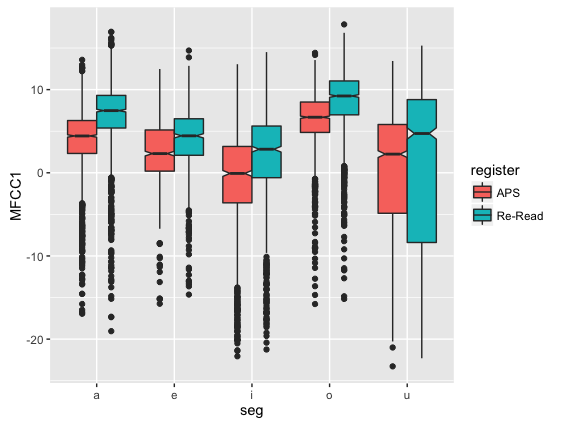
レジスタで色分けして、母音ごとにMFCC1の値をプロット
ggplot(dataV) +

geom_boxplot(aes(y = MFCC1, x = seg, fill = register))

ノッチを加えてプロット*20
ggplot(dataV) +

geom_boxplot(aes(y = MFCC1, x = seg, fill = register), notch = T)

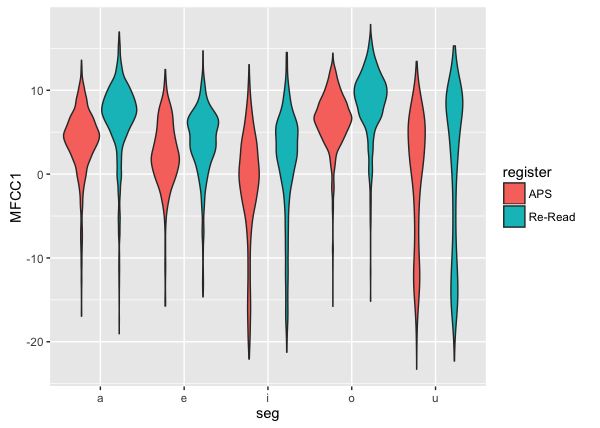
箱ヒゲ図は分布のばらつきを見るのに適していますが、分布の形状（多峰性）については表示しないため注意が必要です（ヒストグラムで検討したような/u/のMFCC1の多峰性については、箱ヒゲ図では確認できません）。分布の形状を確認するには、ヒストグラムを見るか、ヴァイオリンプロットを使います。ヴァイオリンプロットにするには、単に geom_boxplot を geom_violin に書き換えます。
ggplot(dataV) +

geom_violin(aes(y = MFCC1, x = seg, fill = register))

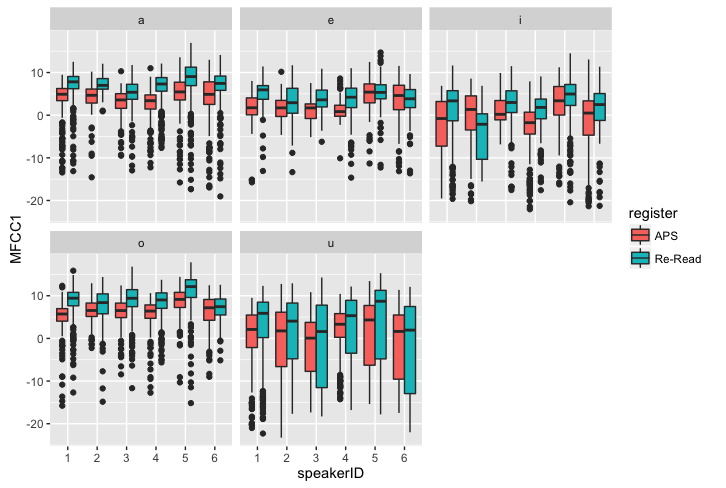
レジスタで色分けして、話者ごとにMFCC1の値をプロットし、母音ごとに並べる
ggplot(dataV) +

geom_boxplot(aes(y = MFCC1, x = speakerID, fill = register)) +

facet_wrap( ~ seg)

ggplotで、異なる列のデータを並べてプロットしたい場合は、reshapeパッケージのmelt関数を使って、データを並び替える必要があります。
dataV.melt <- melt(subset(dataV, select = c(register, speakerID, seg, MFCC1, MFCC2, MFCC3)))

head(dataV.melt)

赤字のメッセージが出ますが問題ありません。dataV.meltの中身を確認してください。カテゴリカル型の列（register, speakerID, seg）はそのまま残りますが、連続型の列は統合されて、新しくできた"variable"列に統合前の列名が、"value"列に数値が入っています。

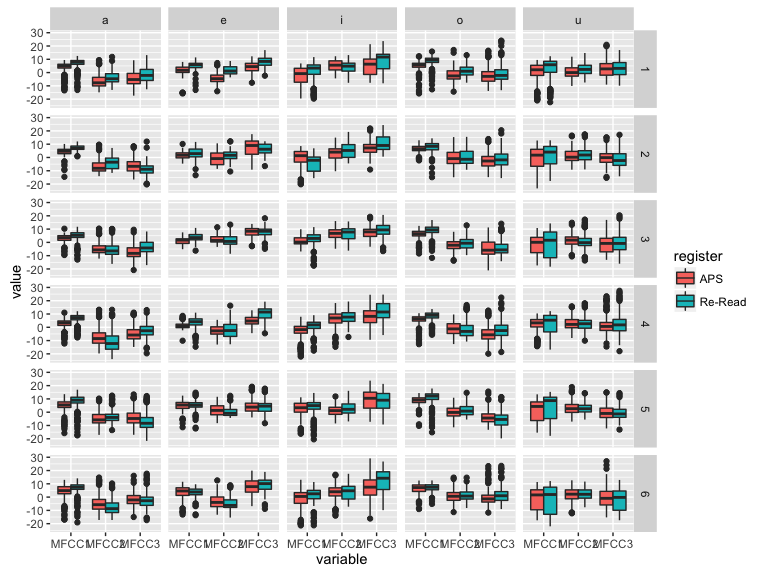
レジスタで色分けして、MFCC1,MFCC2,MFCC3の値をプロットし、話者を縦グリッド、母音を横グリッドに並べる
ggplot(dataV.melt) +

geom_boxplot(aes(y = value, x = variable, fill = register) ) +

facet_grid(speakerID ~ seg)

この例では細かすぎて見づらくなっていますが、違いが出ることを期待しているような条件については、このように並べて検討しておくと良いでしょう。

↑

棒グラフ †

barplot関数を使った方法：バイオスタティスティクス棒グラフが参考になります。

ggplotを使う場合、まずはddplyを使ってデータを集計し、平均値と標準誤差を求めます。自然発話コーパスはデータ数が統制されていないので、どのように集計するか慎重に検討する必要があります。
- 今回は、「各話者・各母音・各レジスター」別にMFCC2とMFCC4の平均値を集計して、その値の「各母音」「各レジスター」について平均値と標準誤差を求めて棒グラフにすることにします。したがって、この棒グラフのエラーバーは話者6名のばらつきを表していることになります。
- 「各話者・各母音・各レジスター」別にMFCC2とMFCC4の平均値を集計します。
  dataVSumm1 = ddply(dataV, c('speakerID', 'seg', 'register'), summarize, MFCC2 = mean(MFCC2), MFCC4 = mean(MFCC4))
  
  dataVSumm1

reshapeパッケージのmelt関数を使って、データを並び替えます。
dataVSumm1M = melt(dataVSumm1)

dataVSumm1M

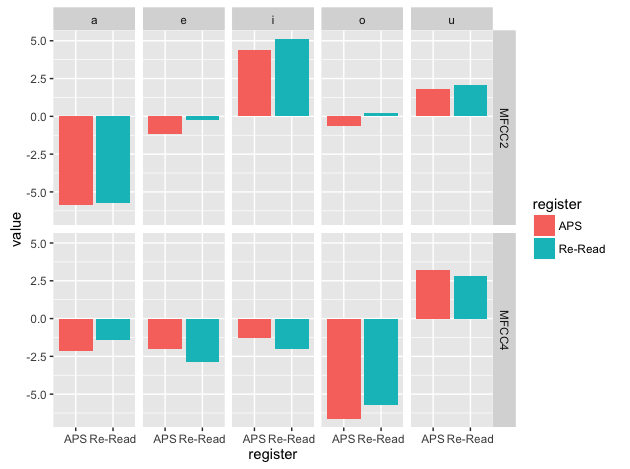
~~エラーバーを表示しないなら、この時点でプロットできます。~~ → 2015/03/12 これは誤りです、すみません。各話者の数値が残っているため、以下の棒グラフは「全話者の合計値」をプロットしています。
qplot(register, weight=value, geom="bar", data=dataVSumm1M, facets = variable ~ seg, fill=register, ylab="value")

エラーバーを表示しないなら、その値の「各母音・各レジスター」について再度MFCC2、MFCC4の平均値のみを求めてプロットします。
dataVSumm2 = ddply(dataVSumm1, c('seg', 'register'), summarize, MFCC2 = mean(MFCC2), MFCC4 = mean(MFCC4))

dataVSumm2

dataVSumm2M = melt(dataVSumm2)

dataVSumm2M

qplot(register, weight=value, geom="bar", data=dataVSumm2M, facets = variable ~ seg, fill=register, ylab="value")

エラーバーを表示する場合、その値の「各母音・各レジスター」についてMFCC2とMFCC4の平均値と標準誤差を求めます。
dataVSumm3 = ddply(dataVSumm1M, c('seg', 'register', 'variable'), summarize, mean = mean(value), sd = sd(value), se = (sd(value)/sqrt(length(value)) ) )

dataVSumm3

length(value)は、集計するデータサイズ。ここでは話者数の6。

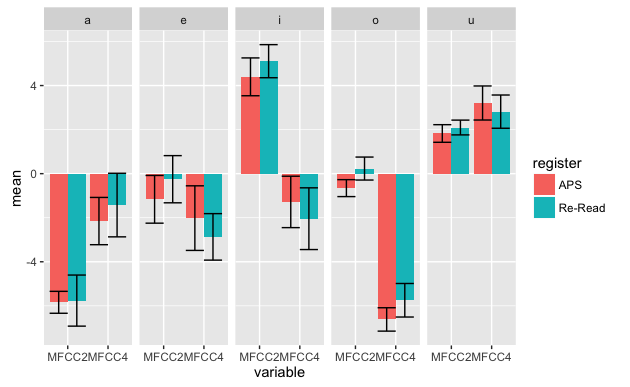
ggplot関数を使って棒グラフとエラーバーを表示します（参考：プログラムは一日にしてならずエラーバーできた）。
ggplot(dataVSumm3, aes(x=variable, y=mean, fill=register)) +

geom_bar(stat="identity", position="dodge") +

geom_errorbar(aes(ymax=mean+se, ymin=mean-se), position="dodge") +

facet_grid( ~ seg)

"aes"の設定はgeom_barでもgeom_errorbarでも共通して使うので、ggplotの中で宣言しておきます。*21

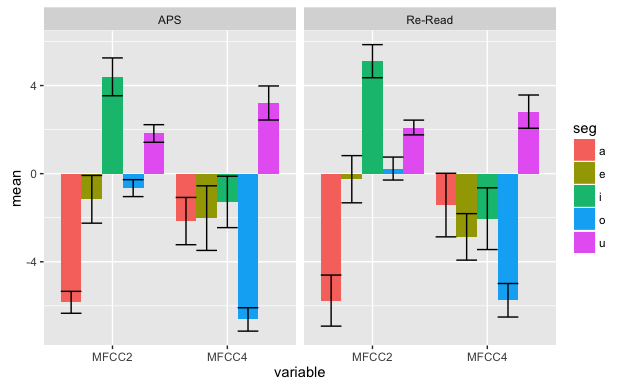
fillとfacetの設定を変えてプロットの形式を変更します。

ggplot(dataVSumm3, aes(x=variable, y=mean, fill=seg)) +

geom_bar(stat="identity", position="dodge") +

geom_errorbar(aes(ymax=mean+se, ymin=mean-se), position="dodge") +

facet_grid( ~ register)

↑

統計解析 †

↑

準備 †

lme4パッケージとlmerTestパッケージのインストールが完了していれば、ライブラリを呼び出すだけでOKです。plyrパッケージ、reshapeパッケージ、pwrパッケージのライブラリも呼び出しておきます。
library(lme4)

library(lmerTest)

library(plyr)

library(reshape)

library(pwr)

サンプルデータ CSJ_MFCC26_short.zip をダウンロードして、データテーブルで読み込んでおきます。
data <- read.table("E:/Users/m-kouki/Desktop/CSJ_MFCC26.txt", header = T)

data$speakerID = factor(data$speakerID)

data$segID = factor(data$segID)

data$frameID = factor(data$frameID)

↑

t検定とパワーアナリシス †

対応のないt検定
- 全てのデータのMFCC5の平均値とMFCC6の平均値の間に、有意な差があるかどうかを調べてみます。
- まずは箱ヒゲ図を書いてみます。
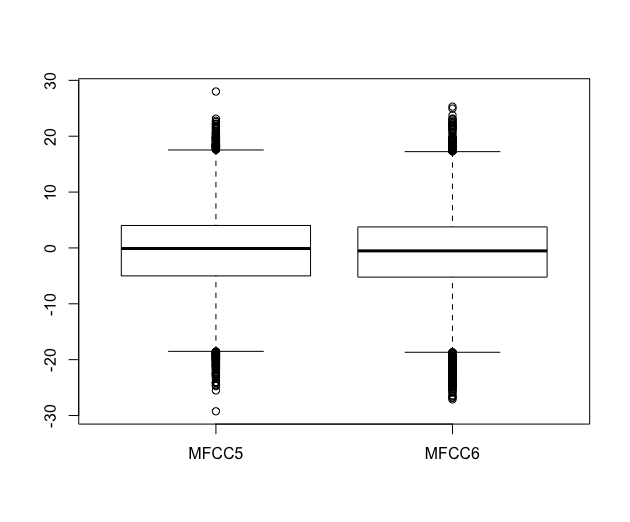
  boxplot(subset(data, select = c(MFCC5, MFCC6) ) )

ほぼボックスが重複しているように見えますが、ノッチが極めて細いため、差があるかもしれません。

F検定で等分散性を見てみます（Rではt.test関数で自動的にやってくれるので必須ではありません）。
var.test(data$MFCC5, data$MFCC6)

	F test to compare two variances

data:  data$MFCC5 and data$MFCC6
F = 1.017, num df = 40137, denom df = 40137, p-value = 0.0908
(略)

p値は0.09なので、ぎりぎりですがMFCC5とMFCC6は「等分散」であると判断できます。

t検定を実施します。ここでは等分散であることを明記します。
t.test(data$MFCC5, data$MFCC6, var.equal=TRUE)

```
	Two Sample t-test

data:  data$MFCC5 and data$MFCC6
t = 5.3208, df = 80274, p-value = 1.036e-07
(略)
```
- p値は0.001より小さいので、MFCC5とMFCC6の平均値は有意に異なると結論できます。
var.equalオプションなしで実行した場合、等分散であればt検定、異分散であればウェルチのt検定が自動的に実行されます。例えば、MFCC4とMFCC9をオプション無しでt検定にかけてみます。*22
t.test(data$MFCC4, data$MFCC9)

```
	Welch Two Sample t-test

data:  data$MFCC4 and data$MFCC9
t = 1.3549, df = 77047.3, p-value = 0.1754
(略)
```
- p値が0.05より大きいので、MFCC4とMFCC9の平均値は有意に異なるとは結論できません。

【注】t検定で比較する2群の標本数が大きく違う場合は、ウェルチのt検定を行うのに加えて、検定力（検出力、パワー）の値を併記したほうが良いようです*23
- 上のデータの検定力を求めてみます。参考：効果量・検定力・サンプルサイズ（高知大村上先生）
- 今回のt検定で使用した２つのデータサイズ確認
  length(data$MFCC4)

```
 [1] 40138
```
length(data$MFCC9)

```
 [1] 40138
```
検定力を求める
pwr.t2n.test(n1=40138, n2=40138, sig.level=0.05, d=0.8)

n1=40138 : データ群1のデータサイズ（サンプル数）です。
n2=40138 : データ群2のデータサイズ（サンプル数）です。今回は両群のデータサイズは同じですが、異なる値を指定することもできます。
d=0.8 : Cohenの効果量d には 0.8 を指定しています。これは大きな差を検出するのに必要な値とのことです。研究分野の慣例によって d の値をいくつにするかは多少異なるようです。
sig.level=0.05 : 有意水準0.05で統計を行う場合を想定しています。

結果は以下の通りです。

    t test power calculation 

            n1 = 40138
            n2 = 40138
             d = 0.8
     sig.level = 0.05
         power = 1
   alternative = two.sided

power は 1 になりました。すなわち100回中統計を実施したら、100回同じ結果になることを意味しています。今回のデータサイズがあれば、統計の結果は十分に安定している（検定力は十分である）ということになります。
power の値は 0.8 以上であれば（100回中80回同じ結果になるのであれば）、検定力は十分であるとみなして良いようです。

有意水準と検定力の関係について：例数設計の基礎第８回 Armitage 勉強会（土居先生）

対応のあるt検定
- 上でMFCC4とMFCC9の平均値に有意差がありませんでしたが、これは全ての話者を混ぜたデータでした。もしかしたら、話者ごとにMFCCの値に個人差があり、そのばらつきのせいで有意な差がなかったのかもしれません。
- そこで、話者ごとにMFCC4とMFCC9の平均値を求めて、その値に対してt検定を実施することにします。
  dataSumm1 <- ddply(data, c('speakerID'), summarize, MFCC4 = mean(MFCC4), MFCC9 = mean(MFCC9) )
  
  dataSumm1

  speakerID       MFCC4       MFCC9
1         1 -0.36694394 -0.67979122
2         2 -0.02150908  0.28991697
3         3  0.23361956 -1.49124097
4         4  0.12591752  0.05997551
5         5 -0.97832807  0.45119489
6         6 -0.09088042 -0.02595399

このデータは、各行が同じ話者から得られたデータなので、対応のあるデータです。そこで、t.test関数のオプション paired=TRUE を指定します。
t.test(dataSumm1$MFCC4, dataSumm1$MFCC9, paired = TRUE)

```
	Paired t-test

data:  dataSumm1$MFCC4 and dataSumm1$MFCC9
t = 0.1191, df = 5, p-value = 0.9098
```
- p値が0.05より大きいので、MFCC4とMFCC9の平均値は有意に異なるとは結論できません。
ただし、今回のデータは、集計前よりもあまりにも数が少なくなっていることに注意する必要があります。元のデータは40138個に対して、集計後はわずか6個です。*24
- ある数のデータセットから得られた統計の結果が信頼のできるものであるかどうかは、パワーアナリシスによって確かめることができますが、ここでは省略します。
もう少し対応のあるデータを増やします。レジスタ・音素・話者別にデータを集計してみます。
dataSumm2 <- ddply(data, c('speakerID', 'register', 'seg'), summarize, MFCC4 = mean(MFCC4), MFCC9 = mean(MFCC9) )

dataSumm2

これでデータ数は454個になりました。対応のあるt検定を実施します。
t.test(dataSumm2$MFCC4, dataSumm2$MFCC9, paired = TRUE)

```
	Paired t-test

data:  dataSumm2$MFCC4 and dataSumm2$MFCC9
t = 2.1648, df = 453, p-value = 0.03093
```
- p値は0.001より小さくなりました。したがって、MFCC4とMFCC9の平均値は有意に異なると結論できます。
このように、特に自然発話データの場合、どのような集計を行ったのかによって統計の結果は変わってきますので、慎重に検討する必要があります。

↑

単回帰分析 †

お題：各音素の持続時間（フレーム数）と、各音素のdMFCC1～dMFCC12の二乗和には有意な相関があるか？
- 音素が長いほど、発音に使える時間に余裕があるので、各音素の音響的な変動量は少なくなる（かも、しれない）
- 分析に使用するデータテーブル dataSumm.SS を作ります。各フレームについてdMFCC1～dMFCC12の二乗和（dMFCC.SquareSum）を求めて、音素ごとにフレーム数とdMFCC.SquareSumの平均値を求めます。
  data$dMFCC.SquareSum <- data$dMFCC1^2 + data$dMFCC2^2 + data$dMFCC3^2 + data$dMFCC4^2 + data$dMFCC5^2 + data$dMFCC6^2 + data$dMFCC7^2 + data$dMFCC8^2 + data$dMFCC9^2 + data$dMFCC10^2 + data$dMFCC11^2 + data$dMFCC12^2
  
  dataSumm.SS <- ddply(data, c('speakerID', 'segID'), summarize, seg.length = length(dMFCC.SquareSum), dMFCC.SquareSum = mean(dMFCC.SquareSum) )
  
  head(dataSumm.SS)

  speakerID segID seg.length dMFCC.SquareSum
1         1  4627          4        54.75966
2         1  4628          2        55.05001
3         1  4629          3        45.30628
4         1  4630          6        46.35851
5         1  4631          6        41.52738
6         1  4632         13        39.62246

ここで、目的変数（従属変数）は dMFCC.SquareSum で、説明変数（独立変数） は seg.length です。
- 単回帰分析では、目的・説明の両変数は正規分布する連続変数である必要があります。ヒストグラムで確認します。
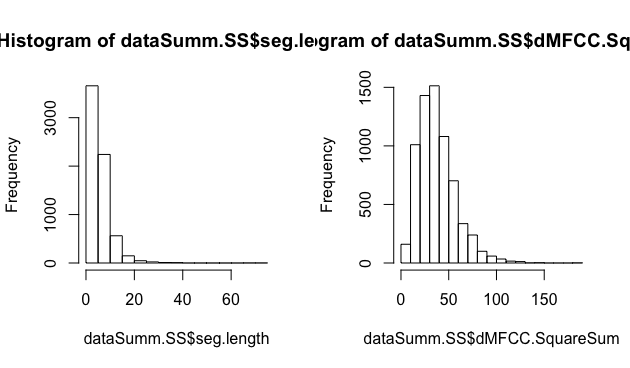
  par(mfrow=c(1,2))
  
  hist(dataSumm.SS$seg.length)
  
  hist(dataSumm.SS$dMFCC.SquareSum)

どちらも、L字型の分布になっています。持続時間や二乗和の値は負値をとらないので、分布に歪みが生じると思われます。とりあえず、対数をとってみます。
dataSumm.SS$seg.length.log = log(dataSumm.SS$seg.length)

dataSumm.SS$dMFCC.SquareSum.log = log(dataSumm.SS$dMFCC.SquareSum)

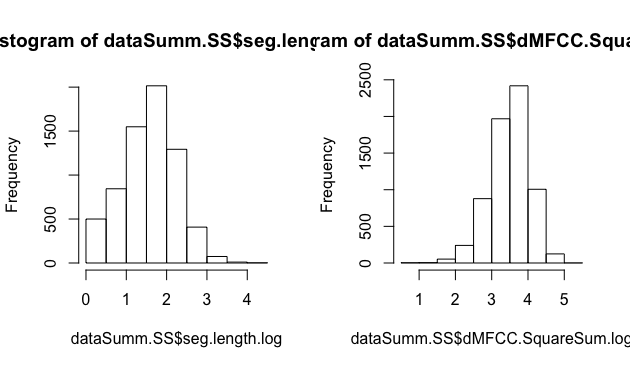
par(mfrow=c(1,2))

hist(dataSumm.SS$seg.length.log)

hist(dataSumm.SS$dMFCC.SquareSum.log)

これで正規分布に近づきました。

続いて、散布図を描いてみます。
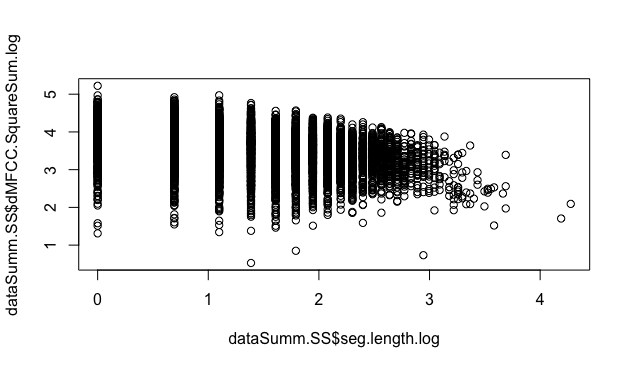
par(mfrow=c(1,1))

plot( dataSumm.SS$seg.length.log, dataSumm.SS$dMFCC.SquareSum.log )

分布が縞々になってしまいました。これは、seg.length が整数値しかとらないことが原因です。seg.length は離散変数の間隔尺度です*25。このようなデータを回帰分析にかけるべきかどうかは慎重に検討する必要がありますが、持続時間を0.01秒ごとに離散化したものがseg.lengthであることから、seg.length.log は正規分布する連続データから、一定・等間隔の尺度で抽出したデータであるとみなして、単回帰にかけても良いと判断しました。

相関分析にかけたところ、有意なある程度の負の相関（p-value < 0.001, 相関係数-0.34）が認められました。
cor.test( dataSumm.SS$seg.length.log, dataSumm.SS$dMFCC.SquareSum.log )

lm関数を使って回帰分析にかけます。
ss.lm <- lm(dMFCC.SquareSum.log ~ seg.length.log, data = dataSumm.SS)

summary(ss.lm)

lm関数の引数で回帰式を指定します。

y(目的変数) = a(切片) + b(傾き)x(説明変数) → y~x 
y = bx → y~-1+x

結果は以下の通りです。

```
Call:
lm(formula = dMFCC.SquareSum.log ~ seg.length.log, data = dataSumm.SS)

Residuals:
     Min       1Q   Median       3Q      Max 
-3.00788 -0.29871  0.07117  0.36034  1.36548 
```
- Residuals（残差）は、データと回帰モデルが予測したの値の差分値です。左から残差の最小値、第１～第３パーセンタイル、最大値が出力されています。個々のデータの残差は residuals 関数で求められます。*26
```
Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)     3.882726   0.014611  265.74   <2e-16 ***
seg.length.log -0.251529   0.008559  -29.39   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.512 on 6693 degrees of freedom
```
- (Intercept) は切片a、seg.length.log は説明変数の傾き（係数）bです。Estimate は推定値、Std. Errorは標準誤差、t valueはt値、Pr(>|t|)は「回帰係数がゼロである」という仮説検定の統計量です。*27
- 目的変数に対して、説明変数 seg.length.log は有意な負の相関があることが確かめられました。
```
Multiple R-squared:  0.1143,	Adjusted R-squared:  0.1142
F-statistic: 863.7 on 1 and 6693 DF,  p-value: < 2.2e-16
```

さきほどの図に回帰直線を追記します。
abline(ss.lm)

回帰診断図を描きます。
par(mfrow=c(2,2))

plot(ss.lm)

↑

一元配置分散分析＋多重比較法 †

この節の手順は誤りがある可能性があります。後ほど書き直します。すみません。

お題：dMFCC1～dMFCC12の二乗和は、母音・ソノラント子音・非ソノラント子音の３群間で有意な違いがあるか？
３群以上の間の有意差の比較は、t検定でなく一元配置分散分析を使います。
- dMFCC1～dMFCC12の二乗和を求め、ここでの議論にもとづき対数をとります（dMFCC.SquareSum.log）。また、音素の種類ラベル（母音, ソノラント子音, 非ソノラント子音）の情報（seg2）を付加します。
  data$dMFCC.SquareSum <- data$dMFCC1^2 + data$dMFCC2^2 + data$dMFCC3^2 + data$dMFCC4^2 + data$dMFCC5^2 + data$dMFCC6^2 + data$dMFCC7^2 + data$dMFCC8^2 + data$dMFCC9^2 + data$dMFCC10^2 + data$dMFCC11^2 + data$dMFCC12^2
  
  data$dMFCC.SquareSum.log <- log(data$dMFCC.SquareSum)
  
  data = transform(data, seg2 = ifelse( ( (seg == "i") | (seg == "e") | (seg == "o") | (seg == "a") | (seg == "u") | (seg == "iH") | (seg == "eH") | (seg == "oH") | (seg == "aH") | (seg == "uH") ) , "vowel", ifelse( ( (seg == "m") | (seg == "n") | (seg == "r") | (seg == "w") | (seg == "y") ) , "sonorant", "non-sonorant" ) ) )
  
  data$seg2 <- factor(data$seg2)
  
  summary(data)

箱ヒゲ図を表示してみます。
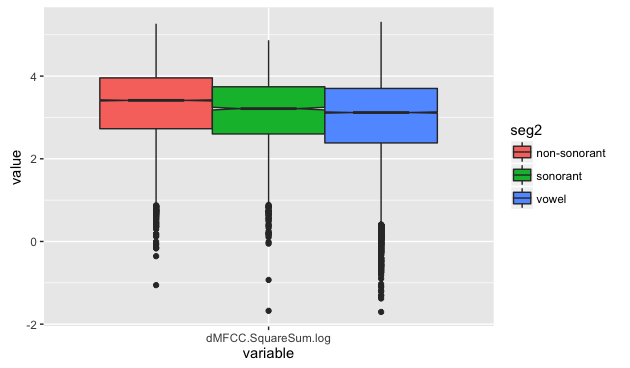
data.melt.aov1 <- melt(subset(data, select = c(seg2, dMFCC.SquareSum.log)))

library(ggplot2)

ggplot(data.melt.aov1) + geom_boxplot(aes(y = value, x = variable, fill = seg2), notch=TRUE )

対応のない一元配置分散分析
- 関数aovを使って分散分析を実行します。
  ss.aov1 <- aov(dMFCC.SquareSum.log ~ seg2, data = data)
  
  ss.aov1

Call:
   aov(formula = dMFCC.SquareSum.log ~ seg2, data = data)

Terms:
                    seg2 Residuals
Sum of Squares   1032.00  33207.52
Deg. of Freedom        2     40135

Residual standard error: 0.9096128
Estimated effects may be unbalanced

分散分析表を見るには、summaryもしくはanova関数を使います。
summary(ss.aov1)

               Df Sum Sq Mean Sq F value Pr(>F)    
seg2            2   1032   516.0   623.6 <2e-16 ***
Residuals   40135  33208     0.8                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

意味は以下の通りです。*28

-------------------------------------------------------
要因    自由度  平方和  平均平方和    F-値     P-値    
-------------------------------------------------------
F            2    1032       516.0   623.6   <2e-16 ***
誤差     40135   33208         0.8                     
-------------------------------------------------------

P値が0.05より小さいため、説明変数（seg2）の各水準（vowel, sonorant, non-sonorant）の平均値に有意差が認められました。

この結果だけでは、どの水準とどの水準に差があったのかは分からないので、各水準間の多重比較を行います。
TukeyHSD(ss.aov1)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = dMFCC.SquareSum.log ~ seg2, data = data)

$seg2
                            diff        lwr        upr p adj
sonorant-non-sonorant -0.1880719 -0.2295339 -0.1466100     0
vowel-non-sonorant    -0.3335195 -0.3556718 -0.3113673     0
vowel-sonorant        -0.1454476 -0.1870469 -0.1038483     0

diff : 平均値の差、lwr : 信頼区間の下限、upr : 信頼区間の上限、p adj : p値
p値がゼロになってしまった。→ 理由は？

R言語で統計解析入門：くり返しのある一元配置分散分析と多重比較(対応なし・標本数が異なる) （福岡大学梶山先生）を参考に、ボンフェローニ法で多重比較を実施。
pairwise.t.test( data$dMFCC.SquareSum.log, data$seg2, p.adjust.method="bonferroni" )

         non-sonorant sonorant
sonorant <2e-16       -       
vowel    <2e-16       <2e-16

各組み合わせについて有意差がある。

対応のある一元配置分散分析
- レジスタ・話者別、また音素の種類ラベル（説明変数）別にデータを集計して、対応のあるデータを作ります。
  library(plyr)
  
  dataSumm.aov1p <- ddply(data, c('speakerID', 'register', 'seg2'), summarize, dMFCC.SquareSum.log = mean(dMFCC.SquareSum.log), seg2 = seg2 )
  
  dataSumm.aov1p

話者について対応をとり分散分析にかける場合、以下のように書きます。
ss.aov1p.speaker <- aov(dMFCC.SquareSum.log ~ seg2 + speakerID, data = dataSumm.aov1p)

summary(ss.aov1p.speaker)

            Df Sum Sq Mean Sq F value   Pr(>F)    
seg2         2 0.6355  0.3177  24.398 7.34e-07 ***
speakerID    5 0.1842  0.0368   2.829   0.0344 *  
Residuals   28 0.3646  0.0130 
(略)

speakerIDの有意な影響が認められます。
多重比較を行います。

TukeyHSD(ss.aov1p.speaker)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = dMFCC.SquareSum.log ~ seg2 + speakerID, data = dataSumm.aov1p)

$seg2
                            diff        lwr         upr     p adj
sonorant-non-sonorant -0.1950974 -0.3103730 -0.07982184 0.0007203
vowel-non-sonorant    -0.3231252 -0.4384008 -0.20784963 0.0000005
vowel-sonorant        -0.1280278 -0.2433034 -0.01275223 0.0271554
(略)

各組み合わせについて有意差がある。

レジスタについて対応をとり分散分析にかける場合、以下のように書きます。
ss.aov1p.register <- aov(dMFCC.SquareSum.log ~ seg2 + speakerID, data = dataSumm.aov1p)

summary(ss.aov1p.register)

            Df Sum Sq Mean Sq F value   Pr(>F)    
seg2         2 0.6355  0.3177  19.276 3.21e-06 ***
register     1 0.0214  0.0214   1.299    0.263    
Residuals   32 0.5275  0.0165

registerの有意な影響は認められません。
多重比較を行います。

TukeyHSD(ss.aov1p.register)

(略)
$seg2
                            diff        lwr           upr     p adj
sonorant-non-sonorant -0.1950974 -0.3238975 -0.0662972987 0.0021341
vowel-non-sonorant    -0.3231252 -0.4519253 -0.1943250881 0.0000020
vowel-sonorant        -0.1280278 -0.2568279  0.0007723138 0.0516484
(略)

registerの有意な影響がないにもかかわらず、レジスタについて対応をとると、母音-ソノラント子音の間の有意差が消えました（有意傾向）。この結果の解釈は難しいです。

speakerIDとregisterを結合して一つのラベル（speakerIDregister）とし、それについて対応をとって分散分析にかけてみます。
dataSumm.aov1p$speakerIDregister = paste(dataSumm.aov1p$speakerID, dataSumm.aov1p$register)

dataSumm.aov1p

ss.aov1p.speakerIDregister <- aov(dMFCC.SquareSum.log ~ seg2 + speakerIDregister, data = dataSumm.aov1p)

summary(ss.aov1p.speakerIDregister)

TukeyHSD(ss.aov1p.speakerIDregister)

結果は省略します。

↑

二元配置分散分析＋交互作用効果の扱い †

この節の手順は誤りがある可能性があります。後ほど書き直します。すみません。

お題：dMFCC1～dMFCC12の二乗和は、母音・ソノラント子音・非ソノラント子音の３群間、及びAPS・Re-Readの２群間で有意な違いがあるか？
- 説明変数（独立変数）が２種類になりました。第１要因は「音素の種類」で３水準（母音・ソノラント子音・非ソノラント子音）を持ちます。第２要因は「レジスタ」で２水準（APS・Re-Read）を持ちます。
- データは一元配置分散分析と同じものを使います。
  data$dMFCC.SquareSum <- data$dMFCC1^2 + data$dMFCC2^2 + data$dMFCC3^2 + data$dMFCC4^2 + data$dMFCC5^2 + data$dMFCC6^2 + data$dMFCC7^2 + data$dMFCC8^2 + data$dMFCC9^2 + data$dMFCC10^2 + data$dMFCC11^2 + data$dMFCC12^2
  
  data$dMFCC.SquareSum.log <- log(data$dMFCC.SquareSum)
  
  data = transform(data, seg2 = ifelse( ( (seg == "i") | (seg == "e") | (seg == "o") | (seg == "a") | (seg == "u") | (seg == "iH") | (seg == "eH") | (seg == "oH") | (seg == "aH") | (seg == "uH") ) , "vowel", ifelse( ( (seg == "m") | (seg == "n") | (seg == "r") | (seg == "w") | (seg == "y") ) , "sonorant", "non-sonorant" ) ) )
  
  data$seg2 <- factor(data$seg2)

交互作用効果をプロットしてみます。
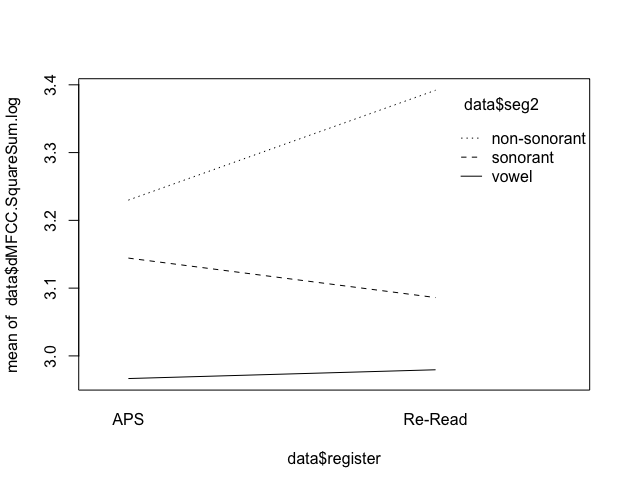
interaction.plot(data$register, data$seg2, data$dMFCC.SquareSum.log)

線が平行でないので、２つの説明変数の間に交互作用がありそうだと分かります。Re-ReadはAPSに比べて、non-sonorantでdMFCCの二乗和が大きく、sonorantでdMFCCの二乗和が小さくなる傾向があります。

対応のない二元配置分散分析
- 関数aovを使って分散分析を実行します。
  ss.aov2 <- aov(dMFCC.SquareSum.log ~ seg2 * register, data = data)
  
  summary(ss.aov2)

「seg2 * register」は、「音素の種類、レジスタ、音素の種類とレジスタを組み合わせた交互作用効果のすべてを含める」という意味です。*29

                 Df Sum Sq Mean Sq F value Pr(>F)    
seg2              2   1034   517.2  627.66 <2e-16 ***
register          1     61    60.7   73.68 <2e-16 ***
seg2:register     2     74    37.0   44.96 <2e-16 ***
Residuals     40132  33070     0.8

交互作用効果は「seg2:register」と表現されます。Pr <2e-16 で、有意な交互作用が認められます。

交互作用効果が確認されたときは、単純（主）効果の検定と多重比較を行います。
- 交互作用効果が有意であった場合、主効果について検討することはあまり意味が無い（場合がある）。
- 交互作用効果が有意でなければ、Tukeyの多重比較法だけでOK。

参考サイト：単純主効果の検定と多重比較（R によるデータの統計的取り扱い）
参考情報：R Note/統計/分散分析

以下、作成中

↑

混合効果モデル：独立変数が一つかつ連続変数 †

混合効果（単）回帰分析
参考：Mixed Effects Models Blog - R言語を用いた混合モデル解析の紹介その1：1要因デザインの場合（２）（理研神長先生）

お題：話者の個人差及び音素の種類の影響を除外してもなお、各音素の持続時間（フレーム数）と、各音素のdMFCC1～dMFCC12の二乗和には有意な相関があるか？
- 単回帰分析のモデルに、ランダム効果（話者の個人差と音素の種類）を加えます。

分析に使用するデータテーブル dataSumm.SS を作ります。各フレームについてdMFCC1～dMFCC12の二乗和（dMFCC.SquareSum）を求めて、音素ごとにフレーム数とdMFCC.SquareSumの平均値を求めます。
data$dMFCC.SquareSum <- data$dMFCC1^2 + data$dMFCC2^2 + data$dMFCC3^2 + data$dMFCC4^2 + data$dMFCC5^2 + data$dMFCC6^2 + data$dMFCC7^2 + data$dMFCC8^2 + data$dMFCC9^2 + data$dMFCC10^2 + data$dMFCC11^2 + data$dMFCC12^2

dataSumm.SS <- ddply(data, c('speakerID', 'seg', 'segID'), summarize, seg.length = length(dMFCC.SquareSum), dMFCC.SquareSum = mean(dMFCC.SquareSum) )

head(dataSumm.SS)

  speakerID seg segID seg.length dMFCC.SquareSum
1         1   a  5169          9        59.40295
2         1   a  5213          7        24.76156
3         1   a  5311         10        27.79712
4         1   a  5325          6        22.73648
5         1   a  5331          8        19.03984
6         1   a  5458         10        46.80528

ここで、目的変数（従属変数）は dMFCC.SquareSum で、説明変数（独立変数） は seg.length、ランダム変数は speakerID と seg です。
重要：ランダム要因はランダムサンプリングされたものにしか使えない*30。例えば、２つの音素を使うように実験を統制したのであれば、segはランダム要因ではありません。

目的・説明の両変数は対数変換します。
dataSumm.SS$seg.length.log = log(dataSumm.SS$seg.length)

dataSumm.SS$dMFCC.SquareSum.log = log(dataSumm.SS$dMFCC.SquareSum)

lmer関数を使ってモデルを構築します。
ss.lmer <- lmer(dMFCC.SquareSum.log ~ seg.length.log + (1 + seg.length.log | speakerID) + (1 + seg.length.log | seg), data = dataSumm.SS)

従属変数 ~ 独立変数　+ (ランダム変数) のように書く。（）でくくったものがランダム変数、くくらないものが独立変数と認識される。
（）の中の｜の左側の数字１は切片を示す。「(1 + seg.length.log | speakerID)」という記述は、ランダム変数 speakerID が、モデルの切片（すなわち、すなわちデータ全体の平均値）と、独立変数 seg.length.log の傾き*31の分散*32に影響を与えると仮定している。

結果は以下の通りです。lmer関数の実行結果はそれだけではp値を出力しませんが、lmerTestパッケージを導入しているとp値も出力してくれます。Mixed Effects Models Blog - R言語を用いた混合モデル解析の紹介その1：1要因デザインの場合（８）、線形混合効果モデル の議論も参照して下さい。
summary(ss.lmer)

Linear mixed model fit by REML 
t-tests use  Satterthwaite approximations to degrees of freedom ['merModLmerTest']
Formula: dMFCC.SquareSum.log ~ seg.length.log + (1 + seg.length.log |      speakerID) + (1 + seg.length.log | seg)
   Data: dataSumm.SS

REML criterion at convergence: 9438.4

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-5.7769 -0.5883  0.0893  0.6904  3.0492 

Random effects:
 Groups    Name           Variance Std.Dev. Corr 
 seg       (Intercept)    0.224867 0.47420       
           seg.length.log 0.038383 0.19592  -0.76
 speakerID (Intercept)    0.007856 0.08864       
           seg.length.log 0.001212 0.03481  -0.58
 Residual                 0.213650 0.46222       
Number of obs: 7101, groups:  seg, 52; speakerID, 6

Fixed effects:
               Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)     3.76566    0.08751 35.49000  43.033  < 2e-16 ***
seg.length.log -0.15318    0.03945 37.86000  -3.883 0.000401 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
            (Intr)
sg.lngth.lg -0.770

各表示の詳細はMixed Effects Models Blog - R言語を用いた混合モデル解析の紹介その1：1要因デザインの場合（７）（理研神長先生）を参照して下さい。
「Fixed effects:」以下が固定因子の効果量。(Intercept) は切片で、Estimate は従属変数の代表値、Std. Errorは従属変数の標準誤差と近い値になるはず（厳密には一致しません）。seg.length.log は独立変数 seg.length.log の傾きで、推定値が-0.15318で、有意な影響が認められます。

文献によっては、「ランダム効果は切片を変数にする場合が多いが、もっと詳しく見たい場合は傾きも推定する」と書かれているものもある。これは逆に言えば、ランダム変数が傾きに与える影響を無視したモデルも考えうるということだろう。
- このようなモデルは以下のようになります。
  ss2.lmer <- lmer(dMFCC.SquareSum.log ~ seg.length.log + (1 | speakerID) + (1 | seg), data = dataSumm.SS)
  
  summary(ss2.lmer)

(略)
REML criterion at convergence: 9542.9
(略)
Fixed effects:
                 Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)       3.74862    0.05653   41.00000   66.31   <2e-16 ***
seg.length.log   -0.17120    0.01106 6872.00000  -15.48   <2e-16 ***
(略)

ランダム変数が切片と傾きに与える影響を考慮したモデル（ss.lmer）と、切片のみに与える影響を考慮したモデル（ss2.lmer）の、どちらが妥当かを調べるには、２つのモデルをanovaにかけます*33。
anova(ss.lmer, ss2.lmer)

```
Models:
..1: dMFCC.SquareSum.log ~ seg.length.log + (1 | speakerID) + (1 | 
..1:     seg)
object: dMFCC.SquareSum.log ~ seg.length.log + (1 + seg.length.log | 
object:     speakerID) + (1 + seg.length.log | seg)
       Df    AIC    BIC  logLik deviance  Chisq Chi Df Pr(>Chisq)    
..1     5 9541.8 9576.1 -4765.9   9531.8                             
object  9 9447.8 9509.6 -4714.9   9429.8 101.95      4  < 2.2e-16 ***
```
- ここで「..1」は ss2.lmer、「object」は ss.lmer です。
- まず、P値（Pr）に着目します。P値が0.05より小さいので、両モデルは有意に異なるといえます。その場合はより情報量の多いモデル（今回は ss.lmer）を選びます。
- P値が0.05より大きい（両モデルに有意な差がない）場合、AICまたはBICの値に注目します。これはモデルの情報量基準で、この値が小さいほど、よりデータに対する適合度が高いモデルであると解釈できます。
- 対数尤度を使ったより厳密なモデル評価の方法は Mixed Effects Models Blog - R言語を用いた混合モデル解析の紹介その1：1要因デザインの場合（５）を参照してください。

まずは、できるだけ情報量の多いモデルを採用するべきです。lmerを実行した結果、以下の警告が出た場合、警告が消えるまでモデルの情報量を削ります。
- Model failed to converge: degenerate Hessian with ○ negative eigenvalues
- Model is nearly unidentifiable: very large eigenvalue
- the random-effects parameters and the residual variance (or scale parameter) are probably unidentifiable
- fixed-effect model matrix is rank deficient so dropping ○ columns / coefficients

↑

混合効果モデル：独立変数が一つかつ離散変数 †

混合効果（一元配置）分散分析
参考：混合モデルを使って反復測定分散分析をする（理研井関先生）
- 混合効果単回帰モデルと同様にモデルを構築して評価します。独立変数内の水準間に有意な差があるかどうか（多重比較検定）は、summary関数またはlmerTestパッケージの step 関数で実施します。

↑

混合効果モデル：独立変数が複数 †

独立変数の性質によって呼び名はいろいろありますが、まとめて扱うことができます。
- 全ての独立変数が連続：混合効果（重）回帰分析
- 全ての独立変数が離散：混合効果（多元配置）分散分析
- 連続・離散の独立変数が混在：混合効果共分散分析

参考：モデルの考え方は混合効果モデル（変量効果モデル、mixed effect model）について、lmerでの書き方は自分用反復測定データにおけるGLMMまとめが参考になります。

分析に使用するデータテーブル dataSumm.SS を作ります。
data$dMFCC.SquareSum <- data$dMFCC1^2 + data$dMFCC2^2 + data$dMFCC3^2 + data$dMFCC4^2 + data$dMFCC5^2 + data$dMFCC6^2 + data$dMFCC7^2 + data$dMFCC8^2 + data$dMFCC9^2 + data$dMFCC10^2 + data$dMFCC11^2 + data$dMFCC12^2

data = transform(data, seg2 = ifelse( ( (seg == "i") | (seg == "e") | (seg == "o") | (seg == "a") | (seg == "u") | (seg == "iH") | (seg == "eH") | (seg == "oH") | (seg == "aH") | (seg == "uH") ) , "vowel", ifelse( ( (seg == "m") | (seg == "n") | (seg == "r") | (seg == "w") | (seg == "y") ) , "sonorant", "non-sonorant" ) ) )

data$seg2 <- factor(data$seg2)

dataSumm.SS <- ddply(data, c('speakerID', 'seg', 'seg2', 'segID', 'register'), summarize, seg.length = length(dMFCC.SquareSum), dMFCC.SquareSum = mean(dMFCC.SquareSum) )

dataSumm.SS$seg.length.log = log(dataSumm.SS$seg.length)

dataSumm.SS$dMFCC.SquareSum.log = log(dataSumm.SS$dMFCC.SquareSum)

お題１：話者の個人差の影響を除外した上で、各音素のdMFCC1～dMFCC12の二乗和 に有意な影響を与えているのは、音素の種類またはレジスタのどちらか（または両方か）？
- ここで、目的変数（従属変数）は dMFCC.SquareSum(.log) で、説明変数（独立変数） は seg および register、ランダム変数は speakerID です。
  - seg と register は離散変数なので、混合効果（二元配置）分散分析のモデルになります。
- lmer関数を使ってモデルを構築します。
  ssANOVA1.lmer <- lmer(dMFCC.SquareSum.log ~ seg * register + (1 + seg * register | speakerID), data = dataSumm.SS)

「*」で繋げられた独立変数は交互作用を考慮します。ここを「+」で繋げた場合は交互作用は考慮されません。
ランダム変数は、切片・各独立変数の傾き・各独立変数の交互作用の傾き全てに影響を与えると仮定しています（フルモデル）。計算にはかなり時間がかかります。
上記のモデルを実行すると、fixed-effect model matrix is rank deficient so dropping 6 columns / coefficients 警告が出ます。そのためモデルを削る必要があります。まずは、ランダム変数の交互作用の傾きに与える影響を除外します。
ssANOVA1_1.lmer <- lmer(dMFCC.SquareSum.log ~ seg * register + (1 + seg + register | speakerID), data = dataSumm.SS)

それでも警告は消えません。続いてランダム変数の傾きを全て除外します。
ssANOVA1_2.lmer <- lmer(dMFCC.SquareSum.log ~ seg * register + (1 | speakerID), data = dataSumm.SS)

それでも警告は消えません。仕方がないので、独立変数同士の交互作用も考慮しないことにします。そこまで削って、ようやく警告が消えました。
ssANOVA1_3.lmer <- lmer(dMFCC.SquareSum.log ~ seg + register + (1 | speakerID), data = dataSumm.SS)

結果は以下で確認できます。詳細は省略します。
anova(ssANOVA1_3.lmer)

summary(ssANOVA1_3.lmer)

step(ssANOVA1_3.lmer)

お題２：話者の個人差の影響を除外した上で、各音素のdMFCC1～dMFCC12の二乗和 に有意な影響を与えているのは、音素の種類（母音・ソノラント子音・非ソノラント子音）またはレジスタのどちらか（または両方か）？
- 目的変数（従属変数）は dMFCC.SquareSum(.log) で、説明変数（独立変数） は seg2 および register、ランダム変数は speakerID です。
- lmer関数を使ってモデルを構築します。
  ssANOVA2.lmer <- lmer(dMFCC.SquareSum.log ~ seg2 * register + (1 + seg2 * register | speakerID), data = dataSumm.SS)

今度は警告は出ませんでした。

結果は以下で確認できます。
anova(ssANOVA2.lmer)

Analysis of Variance Table of type 3  with  Satterthwaite 
approximation for degrees of freedom
               Sum Sq Mean Sq NumDF  DenDF F.value    Pr(>F)    
seg2          110.023  55.011     2 5.8759 199.646 3.966e-06 ***
register        3.356   3.356     1 8.1706  12.178  0.007936 ** 
seg2:register   4.192   2.096     2 7.5733   7.608  0.015430 *

独立変数間の有意な交互作用と、各独立変数の有意な影響が見られます。

単純主効果の確認（≒多重比較）は下記のようにします。
summary(ssANOVA2.lmer)

Linear mixed model fit by REML 
t-tests use  Satterthwaite approximations to degrees of freedom ['merModLmerTest']
Formula: dMFCC.SquareSum.log ~ seg2 * register + (1 + seg2 * register |      speakerID)
   Data: dataSumm.SS

REML criterion at convergence: 11133.4

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-5.2300 -0.6120  0.1008  0.6875  3.1298 

Random effects:
 Groups    Name                         Variance  Std.Dev. Corr                         
 speakerID (Intercept)                  0.0091745 0.09578                               
           seg2sonorant                 0.0070485 0.08396  -0.83                        
           seg2vowel                    0.0003944 0.01986  -0.37  0.28                  
           registerRe-Read              0.0033398 0.05779  -0.88  0.99  0.25            
           seg2sonorant:registerRe-Read 0.0021252 0.04610   0.62 -0.87  0.23 -0.87      
           seg2vowel:registerRe-Read    0.0034361 0.05862   0.64 -0.95 -0.38 -0.90  0.78
 Residual                               0.2755449 0.52492                               
Number of obs: 7153, groups:  speakerID, 6

Fixed effects:
                             Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)                   3.53758    0.04069  4.93800  86.935 4.67e-09 ***
seg2sonorant                 -0.22829    0.04481  4.38000  -5.095  0.00548 ** 
seg2vowel                    -0.22922    0.02024  8.06500 -11.325 3.12e-06 ***
registerRe-Read               0.15976    0.02883  5.23400   5.541  0.00227 ** 
seg2sonorant:registerRe-Read -0.17606    0.04774 11.06100  -3.688  0.00354 ** 
seg2vowel:registerRe-Read    -0.09066    0.03639  6.31300  -2.491  0.04514 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
            (Intr) sg2snr sg2vwl rgsR-R sg2s:R-R
seg2sonornt -0.679                              
seg2vowel   -0.291  0.222                       
registrR-Rd -0.804  0.717  0.295                
sg2snrn:R-R  0.302 -0.651 -0.092 -0.477         
sg2vwl:rR-R  0.486 -0.549 -0.567 -0.741  0.353

もしくは、lmerTestパッケージのstep関数を使います。こちらの方がsummaryよりも時間がかかります。
step(ssANOVA2.lmer)

お題３：話者の個人差及び音素の種類の影響を除外した上で、各音素のdMFCC1～dMFCC12の二乗和 に有意な影響を与えているのは、各音素の持続時間（フレーム数）またはレジスタのどちらか（または両方か）？
- 目的変数（従属変数）は dMFCC.SquareSum(.log) で、説明変数（独立変数） は seg.length(.log) および register、ランダム変数は speakerID と seg です。
  - seg.length.log は連続変数、register は離散変数なので、混合効果共分散分析のモデルになります。
- lmer関数を使ってモデルを構築します。
  ssANCOVA.lmer <- lmer(dMFCC.SquareSum.log ~ seg.length.log * register + (1 + seg.length.log * register | speakerID) + (1 + seg.length.log * register | seg), data = dataSumm.SS)

結果は以下で確認できます。
anova(ssANCOVA.lmer)

Analysis of Variance Table of type 3  with  Satterthwaite 
approximation for degrees of freedom
                        Sum Sq Mean Sq NumDF  DenDF F.value    Pr(>F)    
seg.length.log          3.2454  3.2454     1 38.378 15.8321 0.0002971 ***
register                0.7014  0.7014     1 18.591  3.4218 0.0803016 .  
seg.length.log:register 0.0262  0.0262     1 25.829  0.1280 0.7234587

seg.length.logの有意な影響が見られます。レジスタの影響は認められません。

単純主効果は以下で確認できます。
summary(ssANCOVA.lmer)

(略)
Fixed effects:
                               Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)                     3.72788    0.09773 32.01000  38.144  < 2e-16 ***
seg.length.log                 -0.15572    0.04095 36.29000  -3.803  0.00053 ***
registerRe-Read                 0.13573    0.07338 18.59000   1.850  0.08030 .  
seg.length.log:registerRe-Read -0.01233    0.03447 25.83000  -0.358  0.72347
(略)

↑

ロジスティック回帰分析 †

↑

ロジスティック混合効果モデル †

*1 R Studioであれば、右上の「Environment」>「Import Dataset」でファイルダイアログを起動してファイルを読み込むことも可能です。浅井拓也君、教えてくれてありがとう。
*2 統計学：Rを用いた入門書、Michael J.Crawley 著、野間口謙太郎・菊池泰樹訳、井立出版、2008 より引用
*3 例えば混合モデルの独立変数に指定したとき、連続型変数かカテゴリカル変数かによって結果が変わります。
*4 より詳しくは、R-Source 25. データ型とデータ構造（中央農業総合研究センター竹澤先生）が勉強になります。
*5 この値は音響的特徴の変動量の大きさをあらわしています。
*6 標準化の目的は、各列（各独立変数）の数値のスケールを統一させることで、これは一般化線形モデルを実行する際に必要な手続きのようです。
*7 scale関数の詳細は R-Source 59. 基本統計量の算出（中央農業総合研究センター竹澤先生）が詳しいです。
*8 浅井君、教えてくれてありがとう
*9 Can I calculate z-score with R?を参考にしました。
*10 各話者についてZスコア変換を行う目的は、C0の絶対値の話者による差を無くすためです。話者による個人差がC0に与える影響を無視したい場合、Zスコア変換は有効な方法の一つです。
*11 その音素の時間的中心点が、前後の音素のわたりの影響を最も受けない安定したフレームである、という仮定に基づきます。母音やソノラント子音ではこの仮定は概ね正しいですが、破裂子音などではこの仮定は成り立ちません。
*12 "Error: cannot take a sample larger than the population when 'replace = FALSE'" と表示されます。
*13 浅井君、教えてくれてありがとう
*14 ggplotで同様のことはplotmatricを使えばできたようですが、現在ではGGallyパッケージを使うように要求されます。（参考：美しいペアプロット図を簡単に作る）
*15 ggplotの記法について、浅井拓也君に教えてもらいました。重ねて御礼申し上げます。
*16 本ページは宮島崇浩さんに教えていただきました。ありがとうございます。
*17 統計学：Rを用いた入門書、Michael J.Crawley 著、野間口謙太郎・菊池泰樹訳、井立出版、2008. および Rによるデータサイエンス、金明哲著、森北出版、2007 を参考にしました
*18 R+ 箱ひげ図の読み方を参考にしました。
*19 クォンタイル（分位数）の詳細は四分位数（Wikipedia）を参照してください。
*20 この図にてへこんだ部分がノッチである。これがかぶっていなければ統計的に有意にmedianが違いということが言える。（Seeking for my unique color. [データ解析][R]ノッチの付いたボックスプロットより引用）
*21 浅井拓也君に教えていただきました。ありがとうございます。
*22 実は、MFCC5とMFCC6であっても、オプション無しで実行するとウェルチのt検定が選択されます。F検定のp値がいくつ以上になると通常のt検定が選ばれるのかは、未確認です。
*23 参考：Yahoo!知恵袋「標本数が大きく違う2つのグループで優位差を検定するためにT検定を行った場合、p-valueに歪みが生じる可能性があるのでしょうか？」
*24 nrow(data) と nrow(dataSumm1)で確認できます。
*25 R Note/統計/変数の尺度（データ水準）を参考にしてください
*26 統計学：Rを用いた入門書、Michael J.Crawley 著、野間口謙太郎・菊池泰樹訳、井立出版、2008. および Rによるデータサイエンス、金明哲著、森北出版、2007 を参考にしました
*27 統計学：Rを用いた入門書、Michael J.Crawley 著、野間口謙太郎・菊池泰樹訳、井立出版、2008. および Rによるデータサイエンス、金明哲著、森北出版、2007 より引用しました
*28 分散分析表の枠は一元配置の分散分析（帯広畜産大増田先生）より引用しました。
*29 交互作用効果を含めない場合は「seg2 + register」と記述し、これは対応のある一元配置分散分析と同じです。
*30 馬塚先生のご指摘によります。
*31 t 検定や分散分析で扱う条件間の「差」は混合モデルの回帰方程式における各因子の「係数」、グラフ上の回帰直線の「傾き」に対応する（神長, 井上, 新井, 2012より引用）
*32 固定因子は効果量とその分散を推定するが、ランダム因子は効果量を 0 と仮定して分散のみを推定する（神長, 井上, 新井, 2012より引用）
*33 8b. 統計によれば、この手続きは「呪文」と考えよとのこと。

添付ファイル:

CSJ_MFCC26_short.zip 2765件 [詳細]

Rplot_8.png 2882件 [詳細]

Rplot_15.png 2871件 [詳細]

Rplot_11.png 2944件 [詳細]

Rplot_21.png 2866件 [詳細]

Rplot_20.png 2784件 [詳細]

Rplot_19.png 3002件 [詳細]

Rplot_18.png 2861件 [詳細]

Rplot_17.png 2772件 [詳細]

Rplot_16.png 2777件 [詳細]

Rplot_14a.png 2814件 [詳細]